2セグメントは変速機でした リンクセグメントモデルと運動効率が結びつきます
contents
※2025/11/5 更新
2025/11/5 追記:なんかすごいことを見つけたみたいに書いちゃいましたが、実はそんなすごいことではなく、常識的なことをただ自分なりの解釈で書いているだけかもしれません。まあ、この先の研究で挽回します。
身体運動の効率を完璧に理解したいと思い相変わらず研究をしています。そして今、ようやく答えに直結するであろう最高のひらめきができました。なんと、2セグメントは変速機だったんです。しかも無段の。2セグメントというものすごくシンプルな機構で無段変速機ができあがるんです。響いてください。
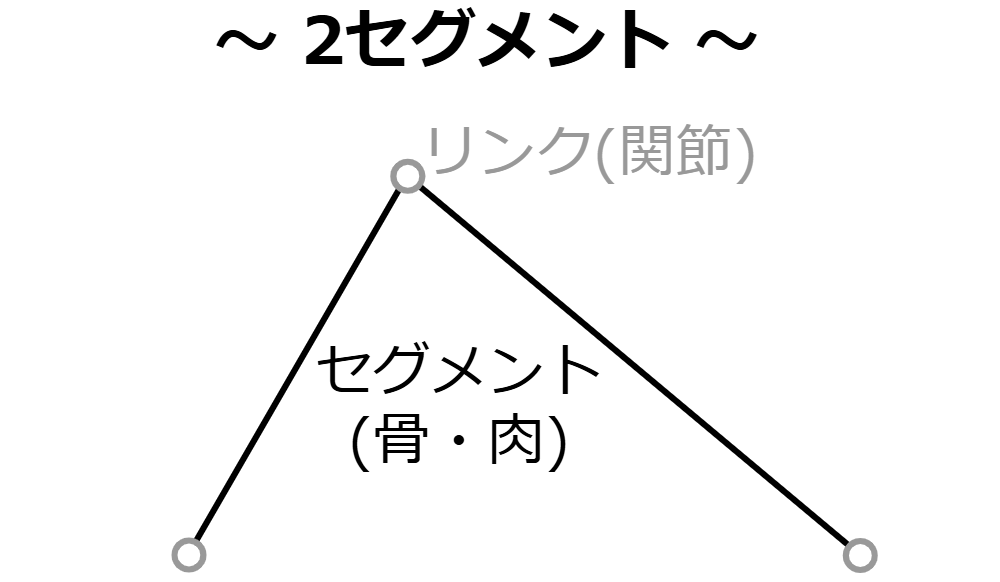
まあ2セグメントが変速機であることが実感できれば、誰でもすごさがわかるはずです。まずは試してほしいです。誰もがやったことがある消しゴムを使って文字を消す動作で、誰もが実感できるので。

消しゴムで消す動作で変速機なことを実感
身体運動の効率と聞くと仰々しいものを思い浮かべてしまいそうますが、消しゴムを使って文字を消す動作などのシンプルなものも身体運動に含まれます。さらに、消しゴムで消す動作を上腕と前腕の2セグメントの動きとして、より単純化してしまいましょう。
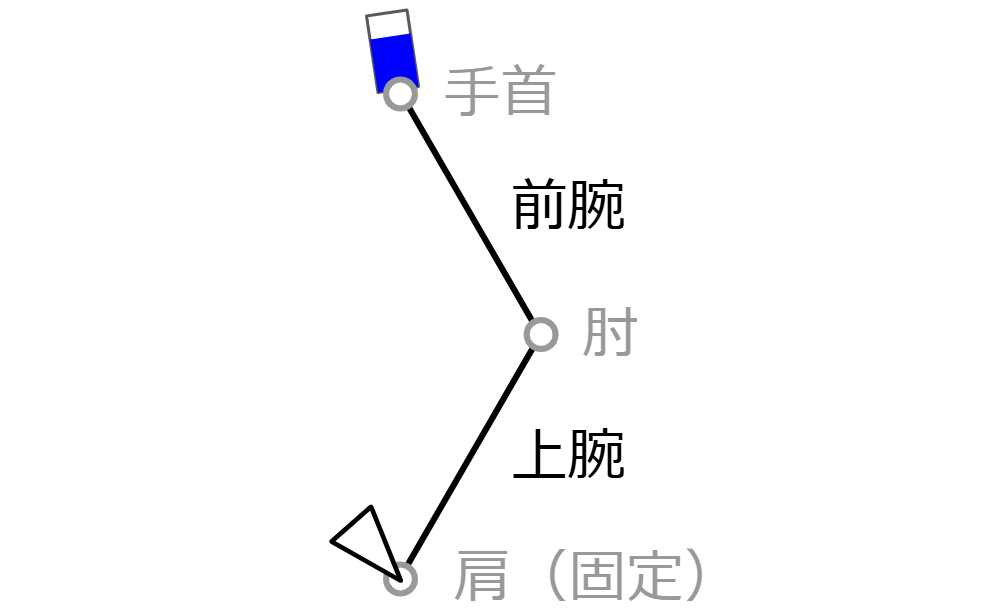
そして、消しゴムを消す動作を思い浮かべるか、実際にやってみてほしいのですが、ほとんどの人は無意識に以下のように上腕と前腕の2セグメントを動かすと思います。
・強い力でないと消せない文字を消すとき
肩と手首を結ぶ直線上を手首が動く。そのとき、上腕と前腕は同じくらい角度が変化する。
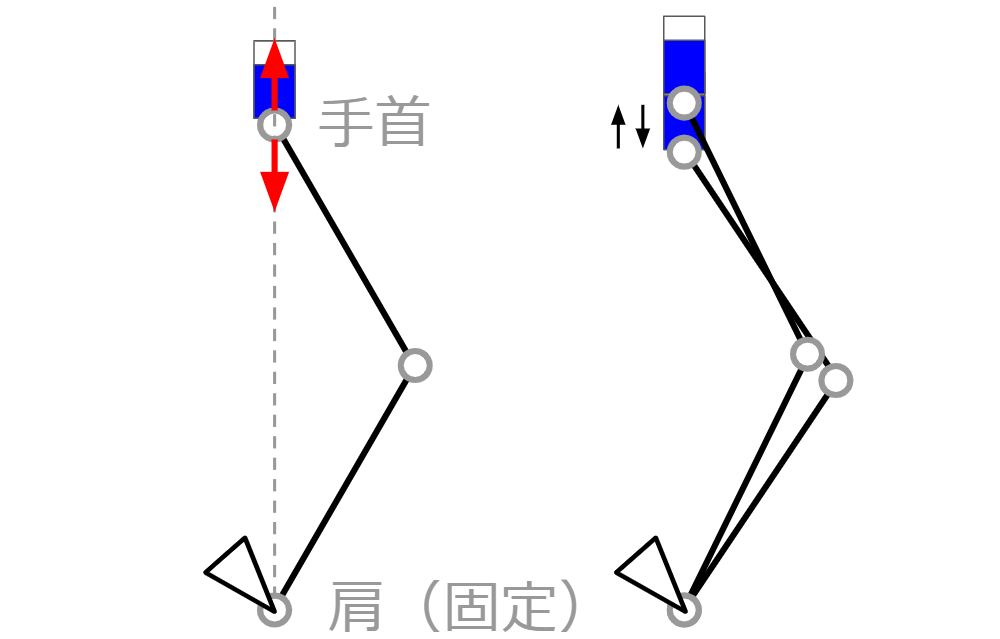
・弱い力でも消せる文字を素早く消したいとき
前腕に直角になる線上を手首が動く。そのとき、上腕はほとんど動かず、前腕の角度が大きく変化する。
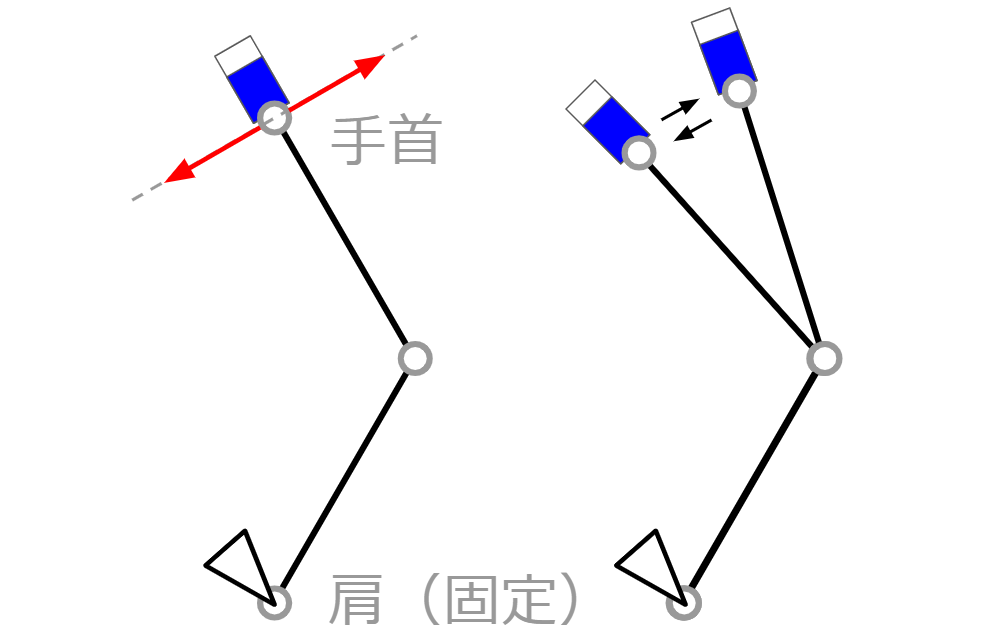
どうでしょうか。このように消しゴムで消すときの動きが変わるのは運動の効率が最適化されているからです。もう少し踏み込んだ説明をします。
2セグメントは、片方の端のリンク(肩)を固定させたときのもう片方の端のリンク(手首)が動く向きによって、強い力で遅く動く(1速寄り)か、弱い力で速く動く(6速寄り)かが変わります。動く向きによって変わるんです。消しゴムで消すときの動作でも、強い力を出したいときは1速寄りの向きに動かし、弱い力でも素早く動かしたいときは6速寄りの向きに動かしているのです。
いやー、ほんと生物って上手いことできてるなあって思います。
ではどの向きに動かせばどのくらい1速寄りもしくは6速寄りになるのでしょうか。それを視覚的に表したのが、たぶん私発のアイデアである「2セグメントジュエル」です。
ここから先は少し難しい話をします。正直言うと面白いパートはここで終わりみたいところはあります。ご視聴ありがとうございました。

2セグメントジュエルの形
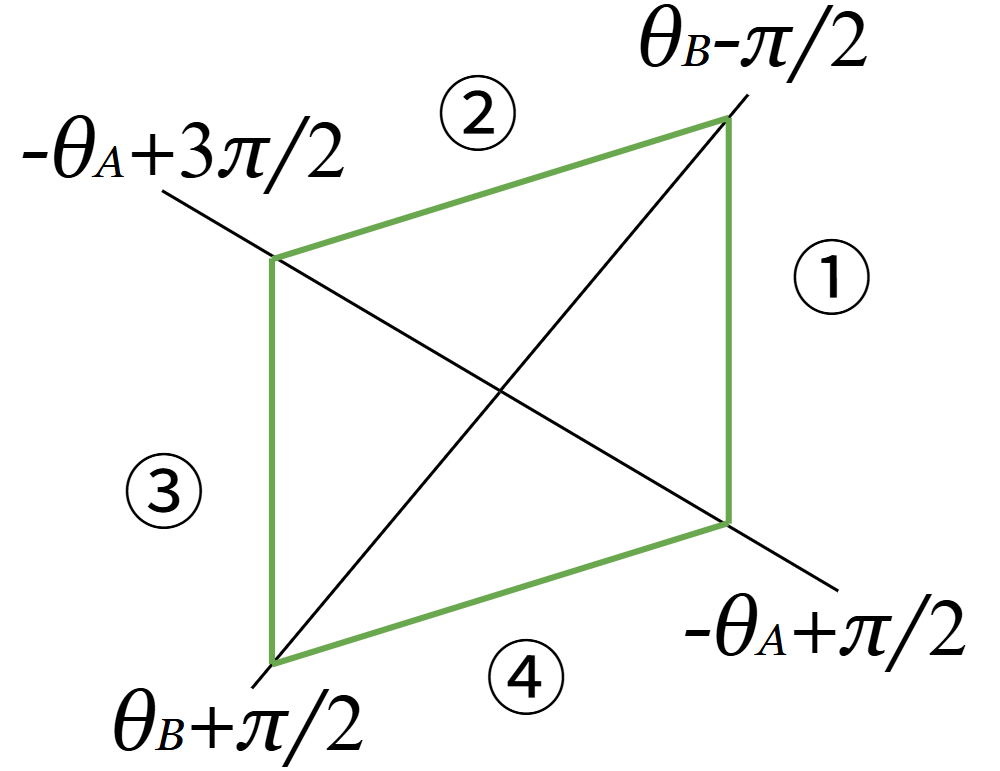
まずは形から入りましょう。2セグメントジュエルは、こんな平行四辺形の形をしています。(2次元の場合。)
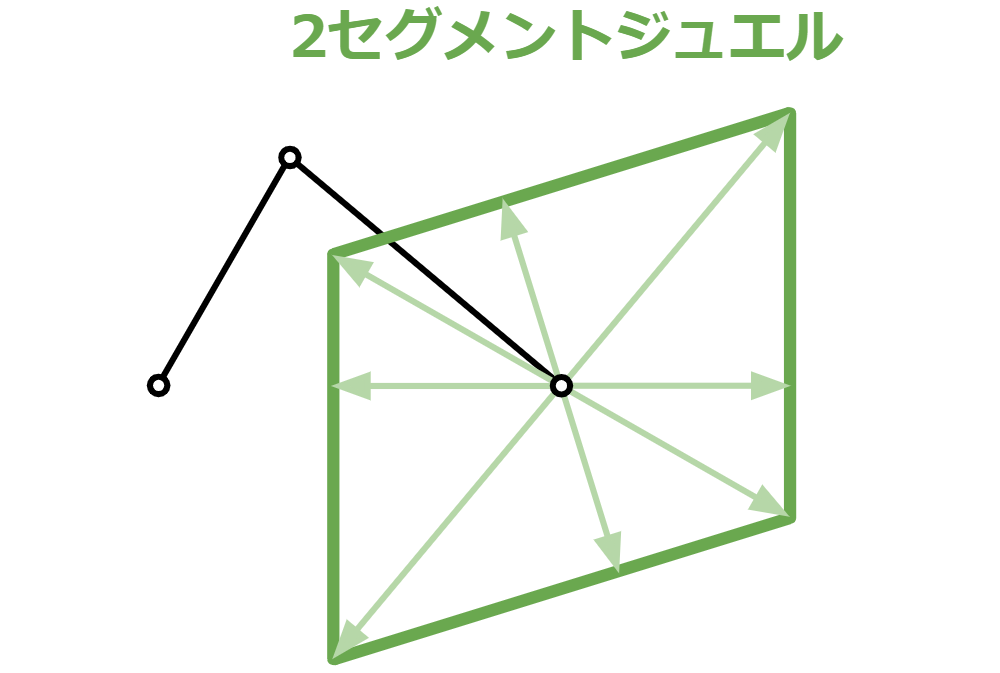
そして、中心から線までの距離が短い向きに動かすと強い力で遅く動き、中心から線までの距離が長い向きに動かすと弱い力で速く動きます。
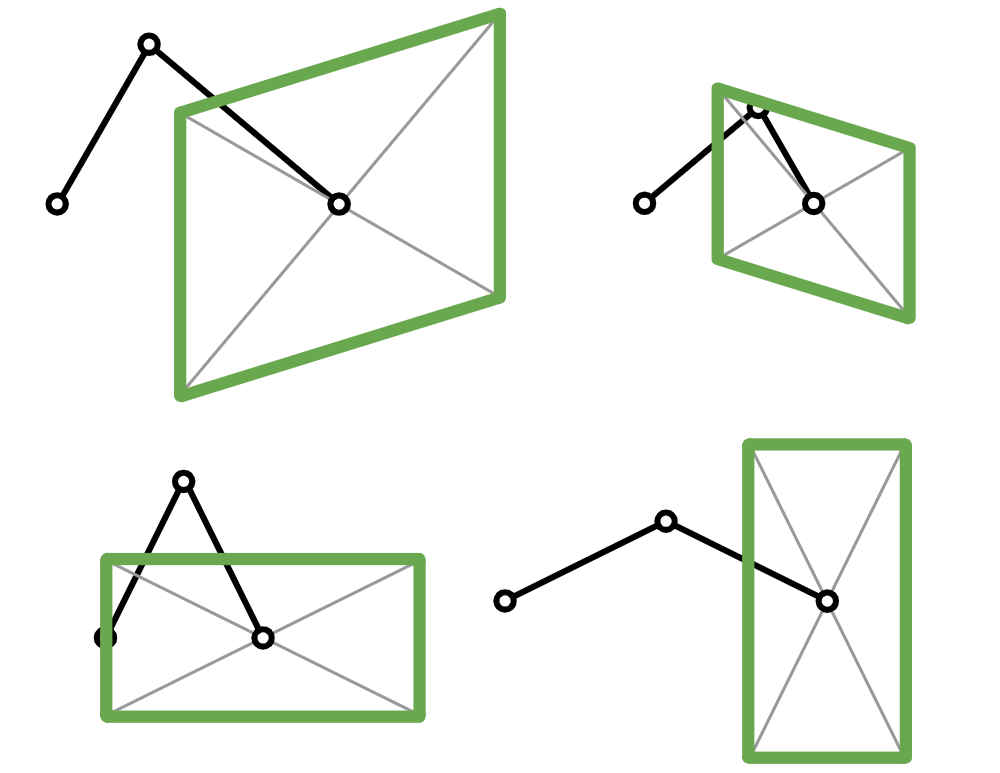
2セグメントジュエルの平行四辺形の形は、2セグメント間の角度やそれぞれのセグメントの長さによって変わります。

2セグメントで行われるパワーの入出力
2セグメントジュエルの2セグメントですが、質量ゼロの単純な2セグメントで考えています。具体的には、下のような感じです。
・それぞれのセグメントの両端がリンク
・それぞれのセグメントの両端にしか外から力・トルクは加わらない(両端でしか外に力・トルクは加えられない)
・それぞれのセグメントは変形しない
・それぞれのセグメントの質量は0
・2セグメントの端のリンクの1つは固定されている
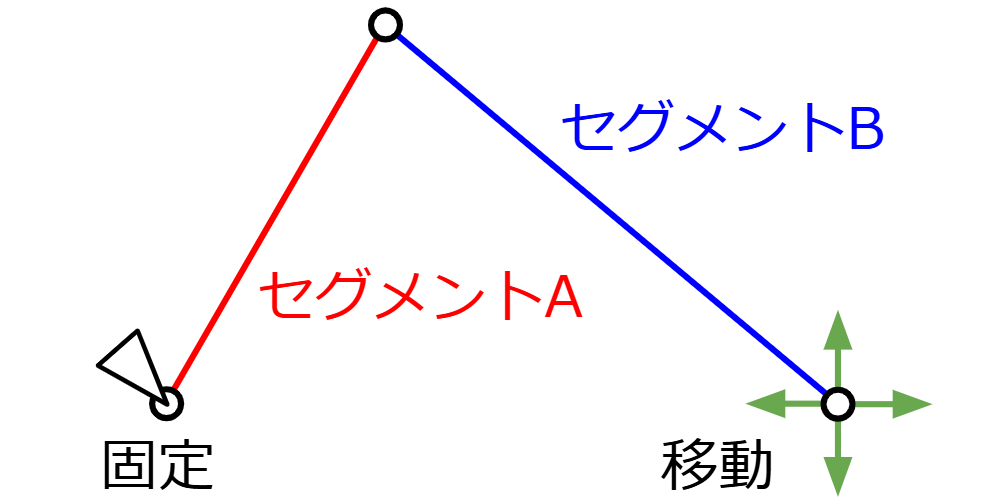
固定されているリンクがある側のセグメントをセグメントA、もう一つのセグメントをセグメントBと呼ぶことにします。
この2セグメントには、トルク・角速度のパワーと力・速度のパワーが出入りします。そして、トルク・角速度のパワー側を入力、力・速度のパワー側を出力として考えたいと思います。
パワーの入力は、「セグメントAに両リンクから加わるトルクベクトルの合計・セグメントAの角速度ベクトル + セグメントBに両リンクから加わるトルクベクトルの合計・セグメントBの角速度ベクトル」となります。パワーの出力は「セグメントB側の端のリンクから外に加える力ベクトル・そのリンクの速度ベクトル」となります。
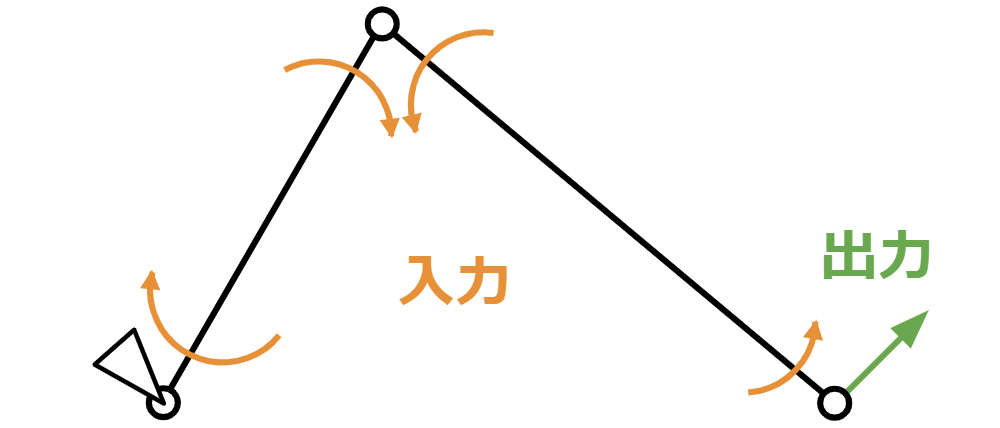
それぞれのセグメントの質量は0であることから、この単純な2セグメントは運動エネルギーも重力による位置エネルギーも含め、エネルギーを持たないことになります。そして、パワーの入力はそのままパワーの出力になり、パワーの入出力が釣り合うことになります。

2セグメントジュエルを導く考え方
同じ動きをする場合、セグメントB側の固定されていない端のリンクをより速く動かすには、より速い角速度の入力が必要になり、セグメントB側の端のリンクで外により強い力を加えるには、より強いトルクの入力が必要になります。速さは角速度に、力はトルクに対応しています。これは直感でもわかると思います。
ただ、消しゴムで消す動作で示したように動きが異なる場合は、同程度の大きさの角速度の入力、同程度の大きさのトルクの入力でも、セグメントB側の端のリンクが外に強い力を加えながら遅く動いたり、外に弱い力を加えながら速く動いたり、ということが起こります。これはセグメントB側の端のリンクが動く向きによって変わります。
実はセグメントB側の端のリンクの動く向きは、2つのセグメントがどのように回転するかで決まります。セグメントAの回転する向き、セグメントBの回転する向き、セグメントAの角速度の大きさとセグメントBの角速度の大きさの割合で決まるのです。
そして面白いことに、セグメントAの角速度の大きさとセグメントBの角速度の大きさの合計が同じでも、向きによってセグメントB側の端のリンクが動く速さが異なります。この性質が2セグメントジュエルの肝の部分です。向きによって速さが異なるのです。
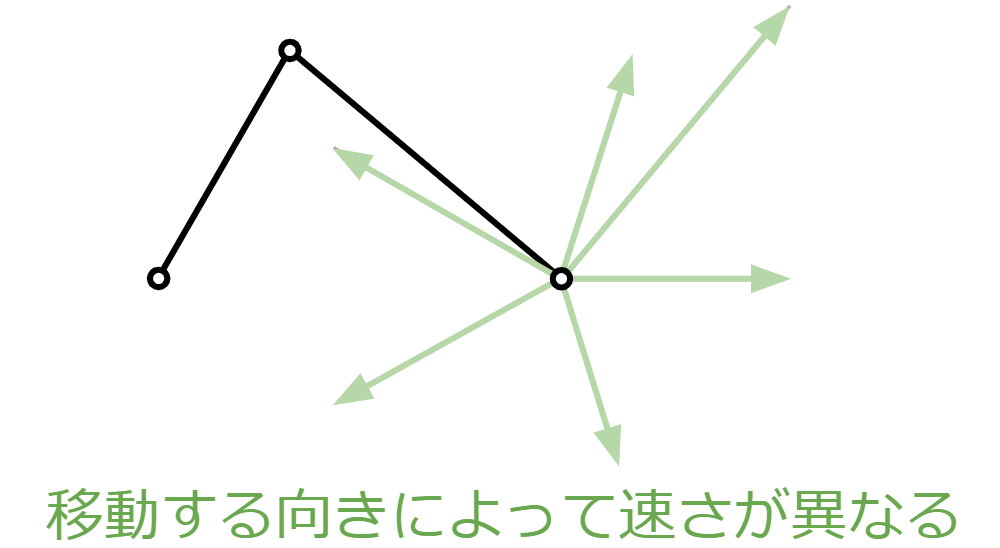
だいぶ2セグメントジュエルっぽくなってきました。ではもう少し具体的に2セグメントジュエルをつくりましょう。
セグメントA、セグメントB合計である微小角度動いたときに、その微小角度に比して、固定されていない端のリンクがどの向きにどれだけ微小移動するかという値は以下の式で得られます。
セグメントB側の端のリンクが微小移動する向きと距離のベクトル[m]/微小角度[rad]
ちなみにこれをジュエルベクトルと言うことにします。ジュエルベクトルを向きごとに求め、すべての向きのジュエルベクトルについて始点を固定して終点をプロットしていくと、2セグメントジュエルを描くことができます。
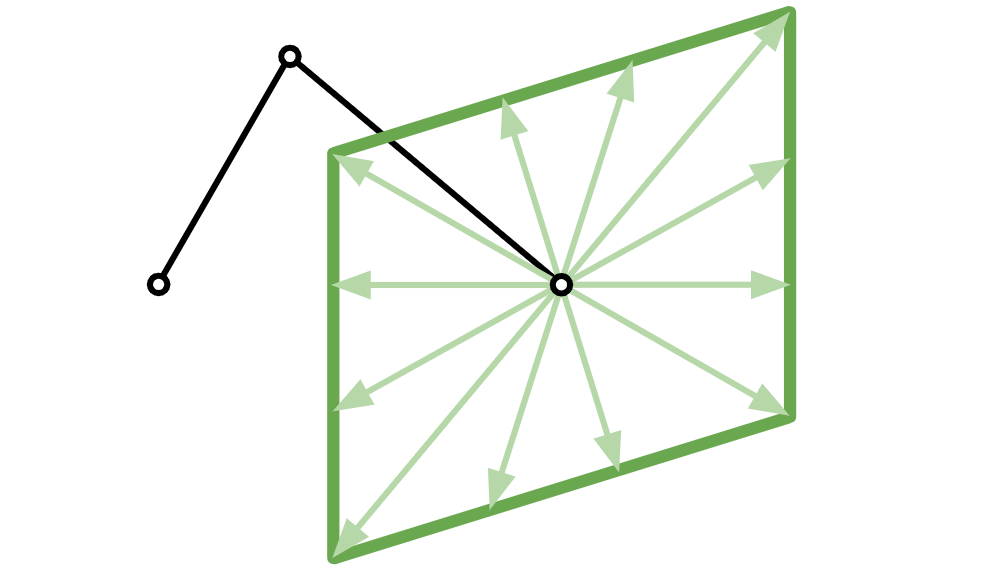

筋肉が発揮するパワーを2セグメントで変速
2セグメントジュエルの中心からの距離が短い向きに動かせば、強い力で遅く動いてパワーを発揮でき、中心からの距離が長い向きに動かせば、弱い力で速く動いてパワーを発揮することができます。
また、パワーの入力を行う筋肉には、ちょうど良くパワーを発揮するための力と速さのバランスがあります。
・入力側の筋肉が発揮するパワーは力と速さのバランスをちょうどよくしたい
・出力側は運動の目的に合った力と速さのバランスでパワーを発揮したい
その両方を結びつけるのが変速機です。2セグメントジュエルで示される変速機としての2セグメントを介して、筋肉のパワー発揮特性と運動の目的に合ったパワー発揮を結びつけるているのです。消しゴムを消すときの動作がまさにこれです。
この変速機としての2セグメントを介した筋肉のパワー発揮特性と運動の目的に合ったパワー発揮の結びつけ、これがうまくできているかどうかが、運動の効率の大部分を決定していると考えています。
この考えが正しければ、謎に包まれていた身体運動の効率の大部分が、2セグメントジュエルを土台とした理論によって計算可能になるのです。これはものすごいことです。

2次元2セグメントジュエルの方程式
一応、2次元の2セグメントジュエルの方程式を導いておきます。実は数式というのはそこまでエラいものではなく、数式の前のアイデアこそが重要なんですね。なのでこれはおまけってことです。
・事前準備
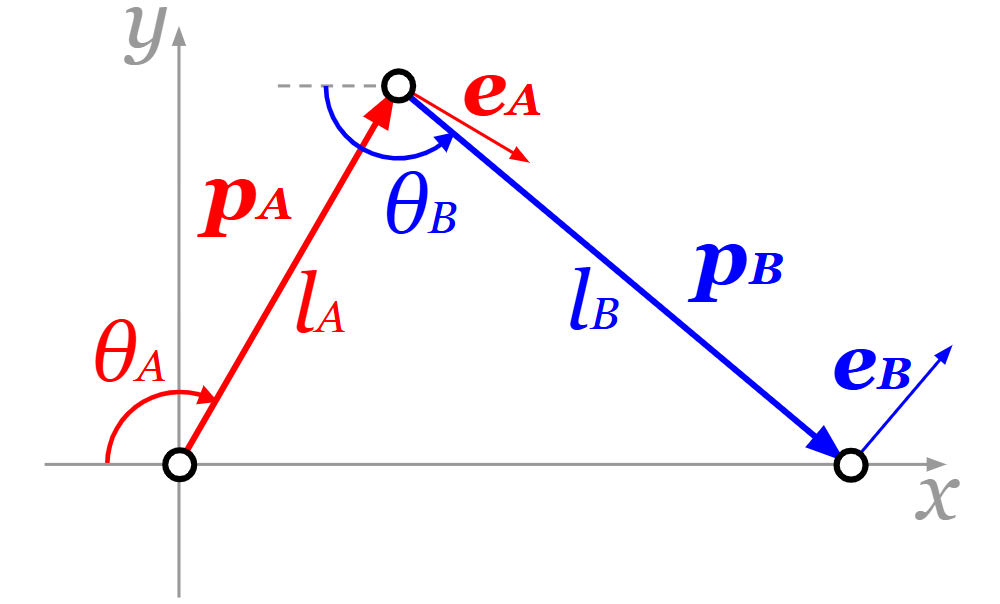
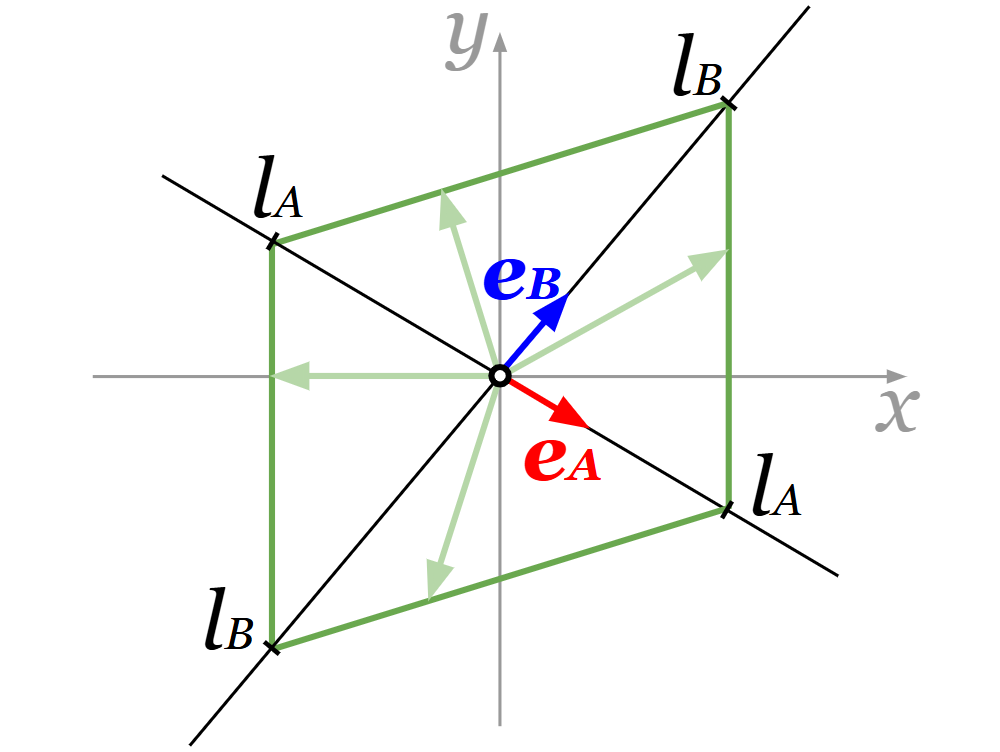
セグメントA側の端のリンクは原点に固定し、セグメントB側の端のリンクを動かすことを考えます。原点(セグメントA側の端のリンク)から見たセグメントB側の端のリンクの向きに\(x\)軸を設定ます。そして、2セグメントの間のリンクの\(y\)座標が正になるように、\(x\)軸と直行する\(y\)軸を設定します。セグメントAの長さを\(l_A \mathrm{\,[m]}\)、セグメントBの長さを\(l_B \mathrm{\,[m]}\)とします。また図のように、セグメントAの角度\(θ_A \mathrm{\,[rad]} \,(0 \lt θ_A \lt π)\)、セグメントBの角度\(θ_B \mathrm{\,[rad]} \,(0 \lt θ_B \lt π)\)、セグメントA側の端のリンクから間のリンクに向かうベクトル\(\boldsymbol{p}_A \mathrm{\,[m]}\)、間のリンクからセグメントB側の端のリンクに向かうベクトル\(\boldsymbol{p}_B \mathrm{\,[m]}\)、\(\boldsymbol{p}_A\)と直行する単位ベクトル\(\boldsymbol{e}_A \mathrm{\,[\,]}\)、\(\boldsymbol{p}_B\)と直行する単位ベクトル\(\boldsymbol{e}_B \mathrm{\,[\,]}\)を設定します。
\(\boldsymbol{e}_A= \begin{pmatrix} \cos (-θ_A+\displaystyle\frac{π}{2}) \\ \sin (-θ_A+\displaystyle\frac{π}{2}) \end{pmatrix} = \begin{pmatrix} \sin θ_A \\ \cos θ_A \end{pmatrix}\)
\(\boldsymbol{e}_B= \begin{pmatrix} \cos (θ_B-\displaystyle\frac{π}{2}) \\ \sin (θ_B-\displaystyle\frac{π}{2}) \end{pmatrix} = \begin{pmatrix} \sin θ_B \\ – \cos θ_B \end{pmatrix}\)
\(l_A \sin θ_A = l_B \sin θ_B\)
となっています。
ここで、微小角度\(Δθ \mathrm{\,[rad]}\)だけセグメントAとセグメントB合計で変化することを考えます。セグメントAの微小の角変位を\(Δθ_A \mathrm{\,[rad]}\)、セグメントBの微小の角変位を\(Δθ_B \mathrm{\,[rad]}\)とすると、下の関係になるということです。
\(Δθ = | Δθ_A | + | Δθ_B | \gt 0\)
パラメータ\(t \mathrm{\,[\,]} \,(0 \leq t \leq 1)\)を使うと、以下のように\(Δθ_A\)、\(Δθ_B\)を表せます。
\(Δθ_A = \pm Δθt\)
\(Δθ_B = \pm Δθ(1-t)\)
この\(t\)はセグメントA、Bどちらがどれだけ角度が変化するかの割合を意味しています。
微小角度\(Δθ\)だけ変化したときの\(\boldsymbol{p}_A\)、\(\boldsymbol{p}_B\)、\(\boldsymbol{p}_A+\boldsymbol{p}_B\)それぞれの微小の変位を\(Δ\boldsymbol{p}_A \mathrm{\,[m]}\)、\(Δ\boldsymbol{p}_B \mathrm{\,[m]}\)、\(Δ(\boldsymbol{p}_A+\boldsymbol{p}_B) \mathrm{\,[m]}\)とすると、下が成り立ちます。
\(Δ(\boldsymbol{p}_A+\boldsymbol{p}_B) = Δ\boldsymbol{p}_A+Δ\boldsymbol{p}_B\)
\(Δ\boldsymbol{p}_A = l_AΔθ_A\boldsymbol{e}_A = \pm l_AΔθt\boldsymbol{e}_A\)
\(Δ\boldsymbol{p}_B = l_BΔθ_B\boldsymbol{e}_B = \pm l_BΔθ(1-t)\boldsymbol{e}_B\)
・ジュエルベクトルの数式
ジュエルベクトル\(\boldsymbol{J} \mathrm{\,[m]}\)は数式で表すと以下のようになります。
\(\boldsymbol{J} = \displaystyle\frac{Δ(\boldsymbol{p}_A+\boldsymbol{p}_B)}{Δθ} = \pm l_At\boldsymbol{e}_A \pm l_B(1-t)\boldsymbol{e}_B\)
① \(Δθ_A \geq 0\)かつ\(Δθ_B \geq 0\)のとき
\(\boldsymbol{J} = l_At\boldsymbol{e}_A + l_B(1-t)\boldsymbol{e}_B\)
② \(Δθ_A \leq 0\)かつ\(Δθ_B \geq 0\)のとき
\(\boldsymbol{J} = – l_At\boldsymbol{e}_A + l_B(1-t)\boldsymbol{e}_B\)
③ \(Δθ_A \leq 0\)かつ\(Δθ_B \leq 0\)のとき
\(\boldsymbol{J} = – l_At\boldsymbol{e}_A – l_B(1-t)\boldsymbol{e}_B\)
④ \(Δθ_A \geq 0\)かつ\(Δθ_B \leq 0\)のとき
\(\boldsymbol{J} = l_At\boldsymbol{e}_A – l_B(1-t)\boldsymbol{e}_B\)
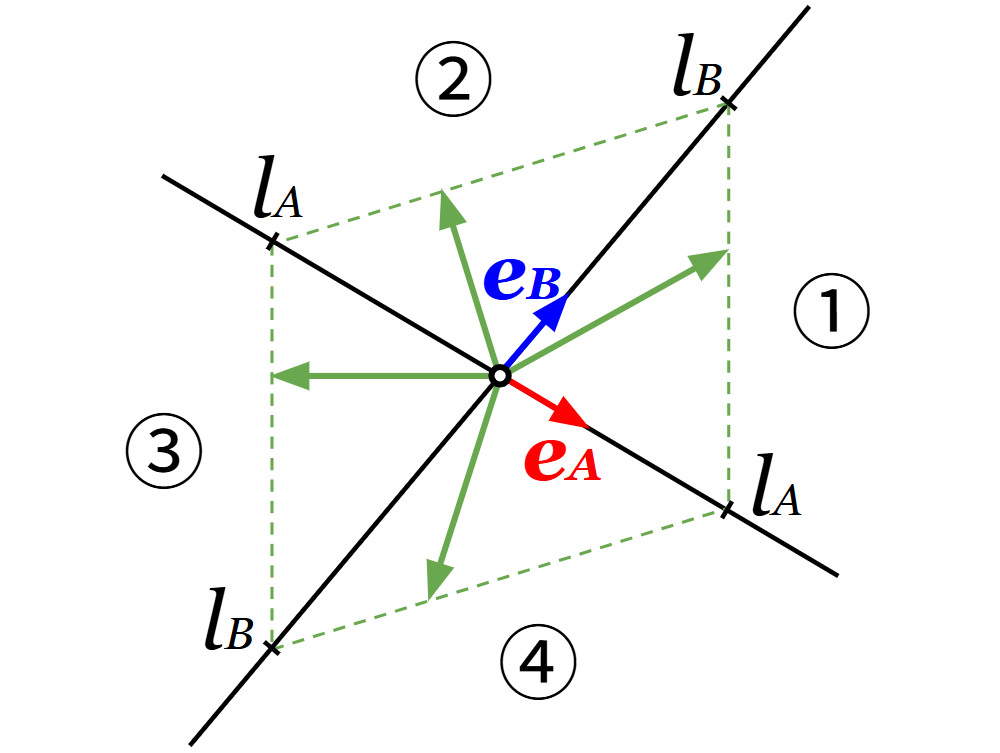
2セグメントジュエルの線は、ジュエルベクトルの始点をある点(原点、\(\boldsymbol{p}_A+\boldsymbol{p}_B\)等)に固定し、パラメータ\(t\)を\(0 \leq t \leq 1\)の範囲で動かしたときの終点をプロットすることで描けます。
・斜交座標での方程式
ジュエルベクトルの始点を原点に固定して描いた2セグメントジュエルの方程式を、斜交座標を用いて表したいと思います。
まず、\(\boldsymbol{e}_A\)の向きに\(x’\)軸を、\(\boldsymbol{e}_B\)の向きに\(y’\)軸を設定します。
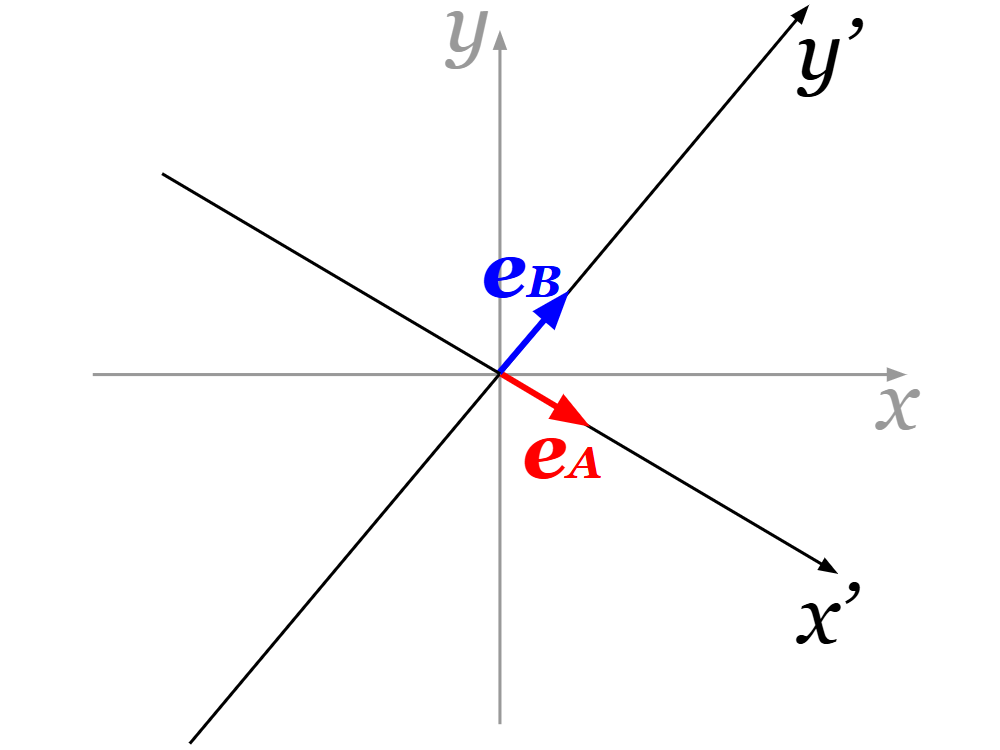
\(x’y’\)斜交座標でジュエルベクトル\(\boldsymbol{J}\)を表すと以下になります。
\(\boldsymbol{J} = \begin{pmatrix} x’ \\ y’ \end{pmatrix}\)
① \(x’ \geq 0\)かつ\(y’ \geq 0\)のとき
\(\boldsymbol{J}(t) = \begin{pmatrix} l_At \\ l_B(1-t) \end{pmatrix}\)
② \(x’ \leq 0\)かつ\(y’ \geq 0\)のとき
\(\boldsymbol{J}(t) = \begin{pmatrix} -l_At \\ l_B(1-t) \end{pmatrix}\)
③ \(x’ \leq 0\)かつ\(y’ \leq 0\)のとき
\(\boldsymbol{J}(t) = \begin{pmatrix} -l_At \\ -l_B(1-t) \end{pmatrix}\)
④ \(x’ \geq 0\)かつ\(y’ \leq 0\)のとき
\(\boldsymbol{J}(t) = \begin{pmatrix} l_At \\ -l_B(1-t) \end{pmatrix}\)
\(t\)を消去して\(y’\)を\(x’\)で表すと以下になります。
① \(x’ \geq 0\)かつ\(y’ \geq 0\)のとき
\(y’ = -\displaystyle\frac{l_B}{l_A}x’ + l_B\)
② \(x’ \leq 0\)かつ\(y’ \geq 0\)のとき
\(y’ = \displaystyle\frac{l_B}{l_A}x’ + l_B\)
③ \(x’ \leq 0\)かつ\(y’ \leq 0\)のとき
\(y’ = -\displaystyle\frac{l_B}{l_A}x’ – l_B\)
④ \(x’ \geq 0\)かつ\(y’ \leq 0\)のとき
\(y’ = \displaystyle\frac{l_B}{l_A}x’ – l_B\)
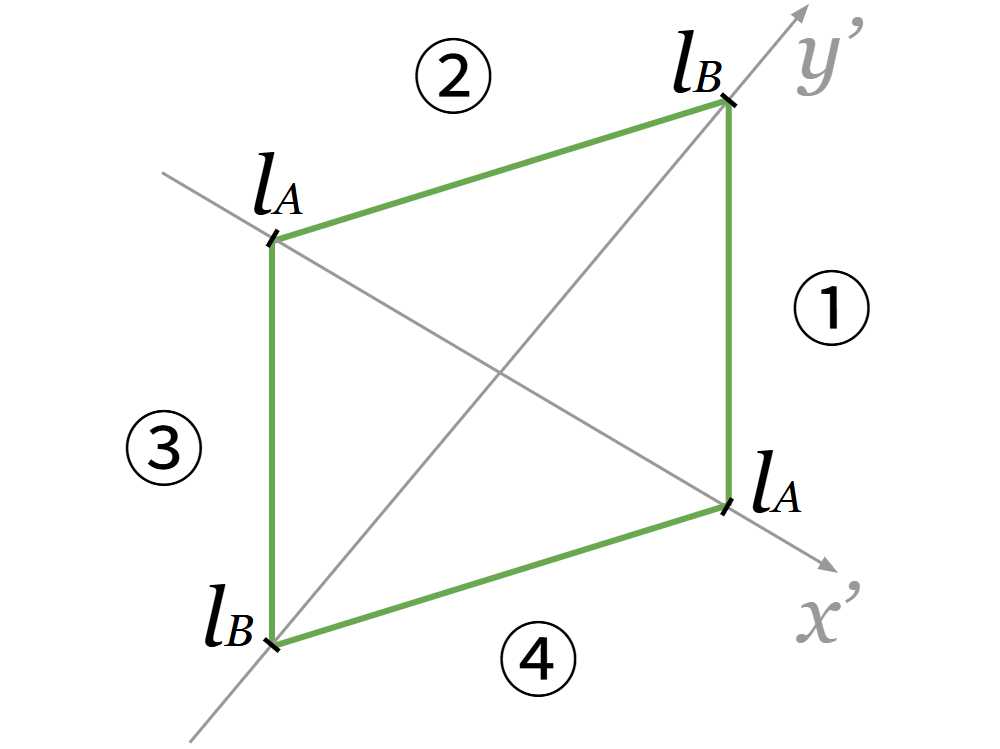
これが斜交座標で表した2セグメントジュエルの方程式です。
・直交座標での方程式
直交座標での2セグメントジュエルの方程式は、斜交座標での方程式を変換する方法で求めることもできます。斜交座標での\(x’\), \(y’\)を直交座標での\(x\), \(y\)を用いて表し、それを斜交座標での方程式に代入すればよいです。
\(x’\),\(y’\)と\(x\),\(y\)の関係は以下になっています。
\(\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} \cos (-θ_A+\displaystyle\frac{π}{2}) & \cos (θ_B-\displaystyle\frac{π}{2}) \\ \sin (-θ_A+\displaystyle\frac{π}{2}) & \sin (θ_B-\displaystyle\frac{π}{2}) \end{pmatrix} \begin{pmatrix} x’ \\ y’ \end{pmatrix}\)
\(\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} \sin θ_A & \sin θ_B \\ \cos θ_A & – \cos θ_B \end{pmatrix} \begin{pmatrix} x’ \\ y’ \end{pmatrix}\)
\(\begin{pmatrix} x’ \\ y’ \end{pmatrix} = {\begin{pmatrix} \sin θ_A & \sin θ_B \\ \cos θ_A & – \cos θ_B \end{pmatrix}}^{-1} \begin{pmatrix} x \\ y \end{pmatrix}\)
最終的に\(x’\), \(y’\)をそれぞれ\(x\),\(y\)で表すと以下になります。
\(x’ = \displaystyle\frac{\cos θ_B}{C}x + \displaystyle\frac{\sin θ_B}{C}y\)
\(y’ = \displaystyle\frac{\cos θ_A}{C}x – \displaystyle\frac{\sin θ_A}{C}y\)
\(C = \sin θ_A \cos θ_B + \cos θ_A \sin θ_B = \sin (θ_A+θ_B)\)
\(C \lt 0\)
これを斜交座標での方程式に代入すると、以下になります。
① \(y \geq \displaystyle\frac{x}{\tan θ_A}\)かつ\(y \leq -\displaystyle\frac{x}{\tan θ_B}\)のとき
\(x = l_A \sin θ_A\)
② \(y \geq \displaystyle\frac{x}{\tan θ_A}\)かつ\(y \geq -\displaystyle\frac{x}{\tan θ_B}\)のとき
\(y = \displaystyle\frac{l_A \cos θ_A – l_B \cos θ_B}{2l_A \sin θ_A}x – \displaystyle\frac{l_A \cos θ_A + l_B \cos θ_B}{2}\)
③ \(y \leq \displaystyle\frac{x}{\tan θ_A}\)かつ\(y \geq -\displaystyle\frac{x}{\tan θ_B}\)のとき
\(x = -l_A \sin θ_A\)
④ \(y \leq \displaystyle\frac{x}{\tan θ_A}\)かつ\(y \leq -\displaystyle\frac{x}{\tan θ_B}\)のとき
\(y = \displaystyle\frac{l_A \cos θ_A – l_B \cos θ_B}{2l_A \sin θ_A}x + \displaystyle\frac{l_A \cos θ_A + l_B \cos θ_B}{2}\)
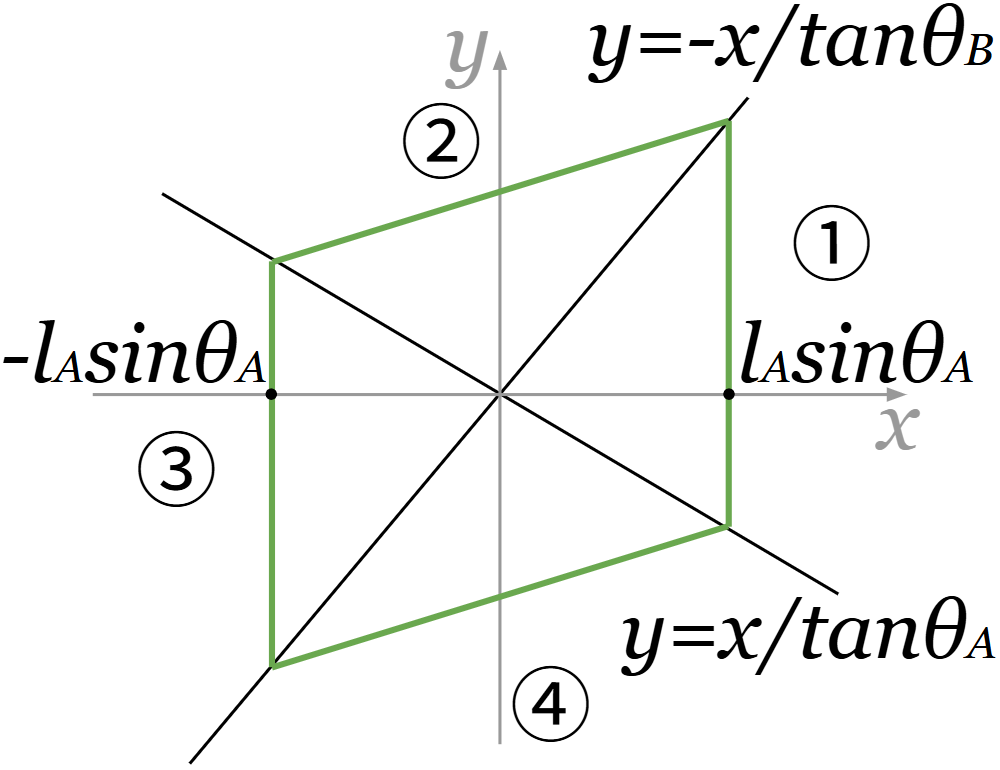
これが直交座標を用いて表した2セグメントジュエルの方程式です。①と③の領域では、2セグメントジュエルの線は\(y軸\)と平行な直線になることが方程式からわかります。
・極座標での方程式
ジュエルベクトルの始点を原点に固定して描いた2セグメントジュエルの方程式を、極座標を用いて表したいと思います。ジュエルベクトルの向きからジュエルベクトルの大きさがすぐにわかるため、最も実用的な形と言えます。
導出過程は省略して、極座標での方程式を示します。
\(\boldsymbol{J} = (r,λ)\)
① \(-θ_A + \displaystyle\frac{π}{2} \leq λ \leq θ_B -\displaystyle\frac{π}{2}\)のとき
\(r = \displaystyle\frac{l_A \sin θ_A}{\cos λ}\)
② \(θ_B -\displaystyle\frac{π}{2} \leq λ \leq -θ_A + \displaystyle\frac{3π}{2}\)のとき
\(r = -\displaystyle\frac{l_A \cos θ_A + l_B \cos θ_B}{ \displaystyle\frac{l_B \cos θ_B – l_A \cos θ_A}{l_A \sin θ_A} \cos λ + 2 \sin λ }\)
③ \(-θ_A + \displaystyle\frac{3π}{2} \leq λ \leq θ_B +\displaystyle\frac{π}{2}\)のとき
\(r = -\displaystyle\frac{l_A \sin θ_A}{\cos λ}\)
④ \(θ_B +\displaystyle\frac{π}{2} \leq λ \leq -θ_A + \displaystyle\frac{5π}{2}\)のとき
\(r = \displaystyle\frac{l_A \cos θ_A + l_B \cos θ_B}{ \displaystyle\frac{l_B \cos θ_B – l_A \cos θ_A}{l_A \sin θ_A} \cos λ + 2 \sin λ }\)
これが極座標を用いて表した2セグメントジュエルの方程式です。
そして、ジュエルベクトル\(\boldsymbol{J}\)は極座標では以下のように表すとします。
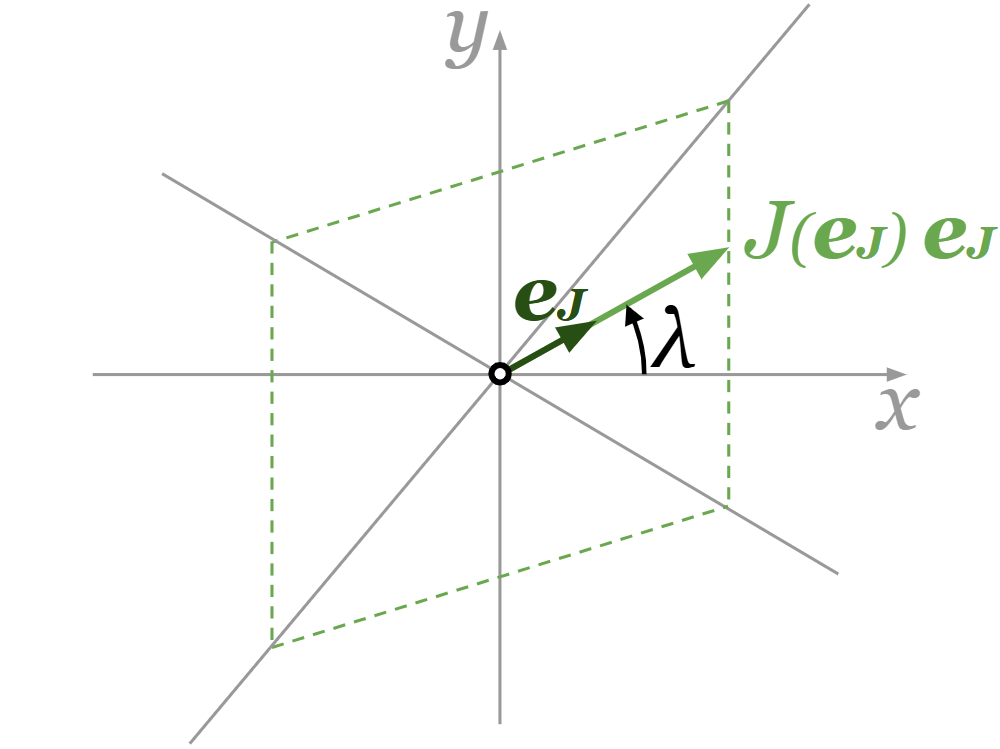
\(\boldsymbol{J} = J(\boldsymbol{e}_J) \boldsymbol{e}_J = (J(λ),λ)\)
直交座標では以下のようになります。
\(\boldsymbol{J} = J(\boldsymbol{e}_J) \boldsymbol{e}_J = J(λ) \begin{pmatrix} \cos λ \\ \sin λ \end{pmatrix}\)
\(\boldsymbol{e}_J \mathrm{\,[\,]}\)はジュエルベクトルの向きの単位ベクトルで、\(λ \mathrm{\,[rad]}\)はジュエルベクトルの向きを示す角度です。\(J \mathrm{\,[m]}\)はジュエルベクトルの向きによって変化するジュエルベクトルの大きさです。
ジュエルベクトルの大きさ\(J(λ)\)は以下のようになっています。
① \(-θ_A + \displaystyle\frac{π}{2} \leq λ \leq θ_B -\displaystyle\frac{π}{2}\)のとき
\(J(λ) = \displaystyle\frac{l_A \sin θ_A}{\cos λ}\)
② \(θ_B -\displaystyle\frac{π}{2} \leq λ \leq -θ_A + \displaystyle\frac{3π}{2}\)のとき
\(J(λ) = -\displaystyle\frac{l_A \cos θ_A + l_B \cos θ_B}{ \displaystyle\frac{l_B \cos θ_B – l_A \cos θ_A}{l_A \sin θ_A} \cos λ + 2 \sin λ }\)
③ \(-θ_A + \displaystyle\frac{3π}{2} \leq λ \leq θ_B +\displaystyle\frac{π}{2}\)のとき
\(J(λ) = -\displaystyle\frac{l_A \sin θ_A}{\cos λ}\)
④ \(θ_B +\displaystyle\frac{π}{2} \leq λ \leq -θ_A + \displaystyle\frac{5π}{2}\)のとき
\(J(λ) = \displaystyle\frac{l_A \cos θ_A + l_B \cos θ_B}{ \displaystyle\frac{l_B \cos θ_B – l_A \cos θ_A}{l_A \sin θ_A} \cos λ + 2 \sin λ }\)

3次元2セグメントジュエルの方程式
まだおまけの数式パートは続きます。今度は3次元で考えます。実際の運動は3次元なので、2次元で考えた2セグメントジュエルを3次元まで拡張しないといけません。そして初めに言っておきます。まだ3次元2セグメントジュエルの方程式、そして3次元2セグメントジュエルの形はわかっていません。私の計算力の無さが原因です。ただし、どのように導けばいいかはある程度わかっているつもりなので、それを説明したいと思います。
・余回転について
基本的な考え方は2次元と同じですが、3次元に拡張するときに注意点が1つだけあります。それは、\(x\)軸周りの回転は端のリンクの移動がなくパワーの入出力もないので、無駄な\(x\)軸周りの回転時に発生するそれぞれのセグメントの角度の変化は、2セグメントジュエルを考えるときの微小角度\(Δθ\)に含めないようにする必要があるということです。この無駄な\(x\)軸周りの回転を「余回転」と言うことにします。余回転については数式に組み込むときに詳しく説明します。
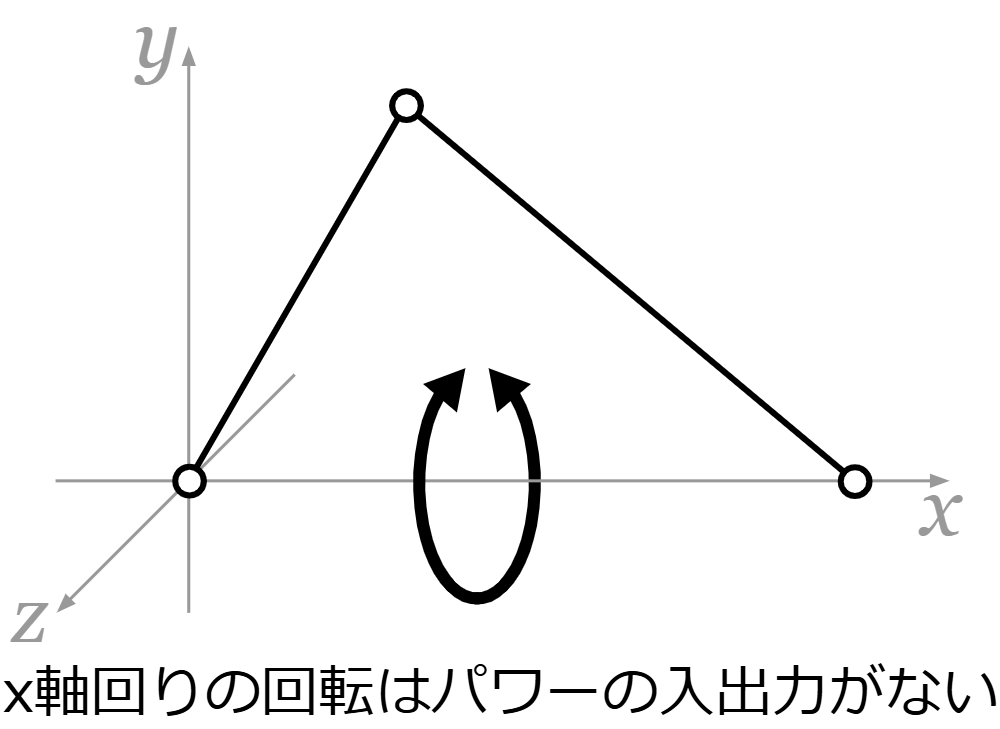
2025/10/16 追記:
余回転には、それぞれのセグメントの長軸(セグメントの両端のリンクを通る軸)周りの回転も含みます。
・事前準備
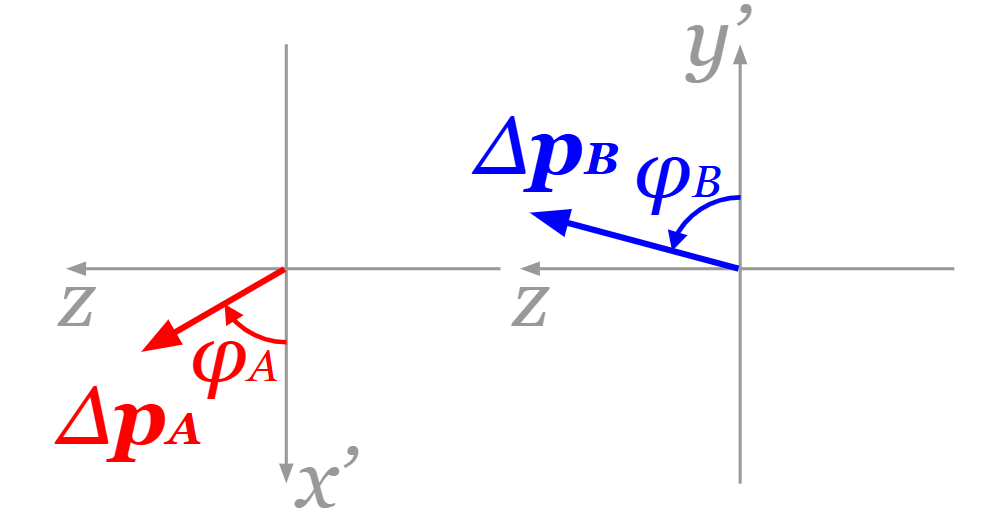
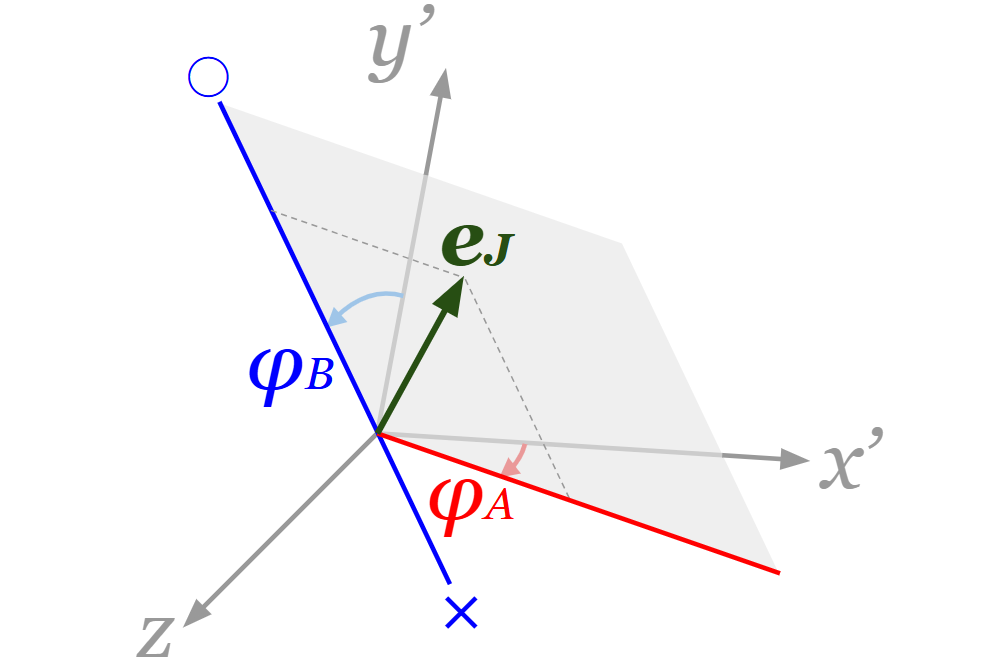
2次元と同じものは省略して、3次元特有のものだけ書いていきます。\(x\)軸と\(y\)軸に直行する\(z\)軸、そして\(x’\)軸、\(y’\)軸を図のように設定します。\(x’\)軸の向きは\(\begin{pmatrix} \sin θ_A \\ \cos θ_A \\ 0 \end{pmatrix}\)、\(y’\)軸の向きは\(\begin{pmatrix} \sin θ_B \\ – \cos θ_B \\ 0 \end{pmatrix}\)となっています。
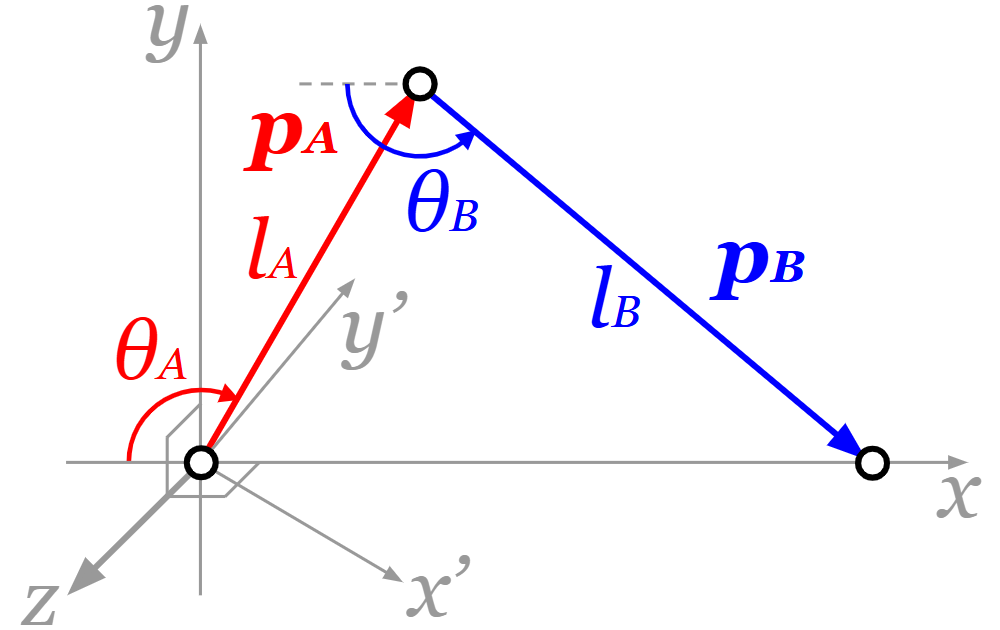
2次元では原点を始点としたときの\(Δ\boldsymbol{p}_A\)、\(Δ\boldsymbol{p}_B\)はそれぞれ\(x’\)軸上、\(y’\)軸上にありましたが、3次元ではそれぞれ\(x’z\)平面上、\(y’z\)平面上にあります。そして図のように\(Δ\boldsymbol{p}_A\)が\(x’\)軸正の向きとなす角\(φ_A \mathrm{\,[rad]}\)、\(Δ\boldsymbol{p}_B\)が\(y’\)軸正の向きとなす角\(φ_B \mathrm{\,[rad]}\)を設定します。
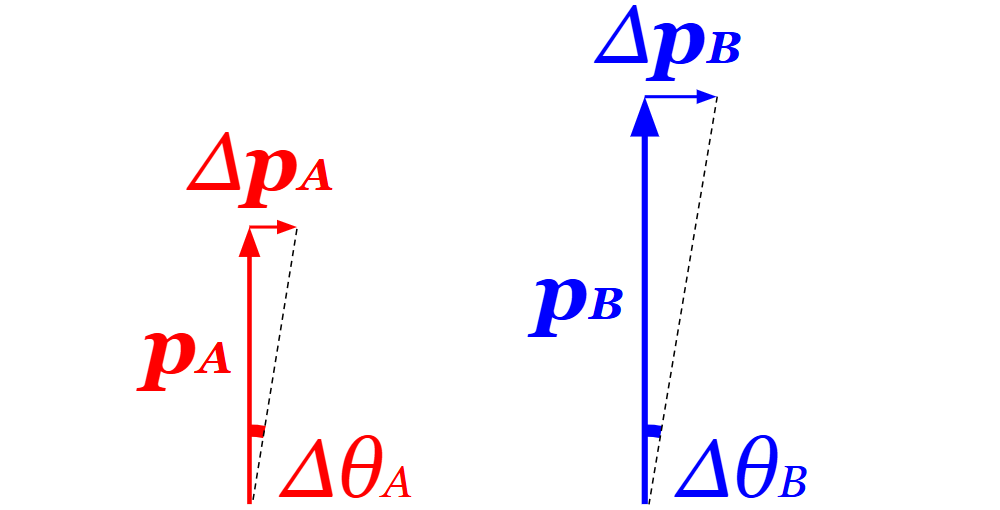
微小角度\(Δθ \mathrm{\,[rad]}\)だけセグメントAとセグメントB合計で変化することを考えます。セグメントAの微小の角変位\(Δθ_A \mathrm{\,[rad]}\)、セグメントBの微小の角変位\(Δθ_B \mathrm{\,[rad]}\)を図のように設定します。
2025/10/16 追記&修正:
セグメントAの長軸周りの微小の角変位\(Δθ_A^* \mathrm{\,[rad]}\)、セグメントBの長軸周りの微小の角変位\(Δθ_B^* \mathrm{\,[rad]}\)を設定します。
\(Δθ_A \geq 0\)
\(Δθ_A^* \geq 0\)
\(Δθ_B \geq 0\)
\(Δθ_B^* \geq 0\)
\(sΔθ = Δθ_A + Δθ_B\)
\(s = \displaystyle\frac{Δθ_A + Δθ_B}{ \sqrt{ {Δθ_A}^2 + {{Δθ_A}^*}^2 } + \sqrt{ {Δθ_B}^2 + {{Δθ_B}^*}^2 } }\)
\(0 \leq s \leq 1\)
となります。パラメータ\(t \mathrm{\,[\,]} \,(0 \leq t \leq 1)\)を使うと、以下のように\(Δθ_A\)、\(Δθ_B\)を表せます。
\(Δθ_A = Δθst\)
\(Δθ_B = Δθs(1-t)\)
\(Δθ_A \geq 0\)
\(Δθ_B \geq 0\)
\(Δθ = Δθ_A + Δθ_B\)
となります。パラメータ\(t \mathrm{\,[\,]} \,(0 \leq t \leq 1)\)を使うと、以下のように\(Δθ_A\)、\(Δθ_B\)を表せます。
\(Δθ_A = Δθt\)
\(Δθ_B = Δθ(1-t)\)
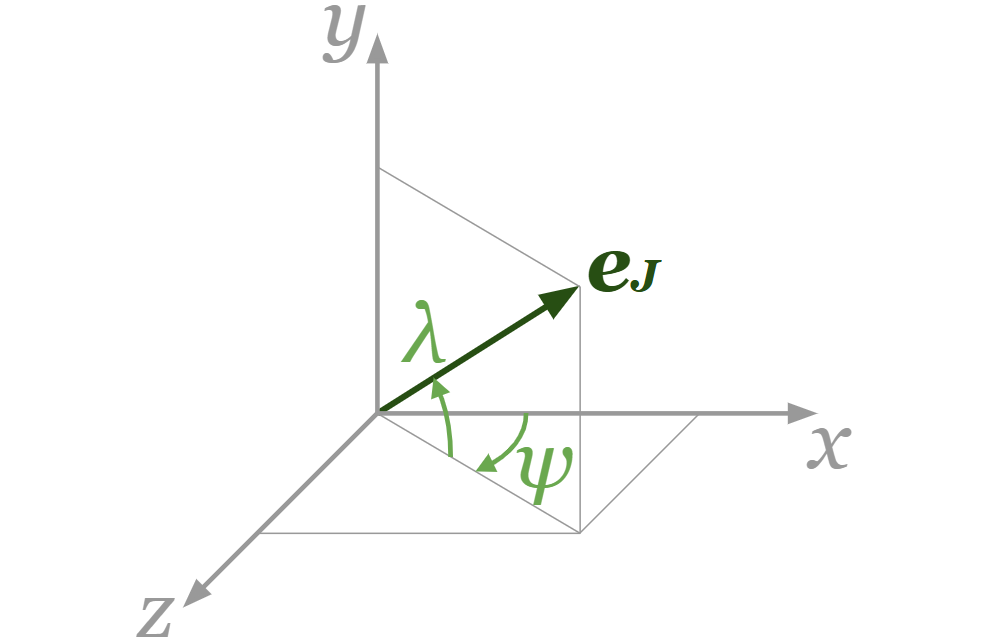
セグメントB側の端のリンクが動く向きに単位ベクトル\(\boldsymbol{e}_J \mathrm{\,[\,]}\)を設定します。また、\(\boldsymbol{e}_J\)の向きを決定する角度\(λ \mathrm{\,[rad]} \,(-\displaystyle\frac{π}{2} \leq λ \leq \displaystyle\frac{π}{2})\)、\(ψ \mathrm{\,[rad]} \,(-π \leq ψ \leq π)\)を図のように設定します。
\(\boldsymbol{e}_J = \begin{pmatrix} \cos λ \cos ψ \\ \sin ψ \\ \sin λ \cos ψ \end{pmatrix}\)
となります。
・ジュエルベクトルと含余回転ジュエルベクトル
含余回転ジュエルベクトル\(\boldsymbol{j} \mathrm{\,[m]}\)というものを考えます。数式で表すと以下のようになります。
\(\boldsymbol{j} = j \boldsymbol{e}_J = \displaystyle\frac{Δ(\boldsymbol{p}_A+\boldsymbol{p}_B)}{Δθ}\)
そして、ある\(\boldsymbol{e}_J\)のときに含余回転ジュエルベクトルの大きさ\(j \mathrm{\,[m]}\)が最大となる含余回転ジュエルベクトルがジュエルベクトル\(\boldsymbol{J} \mathrm{\,[m]}\)になります。
\(J(\boldsymbol{e}_J) = \max \, j(\boldsymbol{e}_J,…)\)
\(\boldsymbol{J} = J(\boldsymbol{e}_J) \boldsymbol{e}_J\)
\(j = J\)ではない含余回転ジュエルベクトルになるような2セグメントの動きは、余回転を含んでいます。微少角度\(Δθ\)のうち、余回転に使われる微少角度は以下のように表せます。
\(\displaystyle\frac{J-j}{J}Δθ\)
・3次元2セグメントジュエルの導き方
ジュエルベクトルの定義から、\(\boldsymbol{e}_J\)が定まればジュエルベクトル\(\boldsymbol{J}\)は一意に定まります。そして\(\boldsymbol{e}_J\)は2つのパラメータ\(λ\)、\(ψ\)で決まります。つまり、ジュエルベクトルも2つのパラメータ\(λ\)、\(ψ\)で決まるということです。3次元の2セグメントジュエルは、ジュエルベクトルの始点をある点(原点等)に固定し、2つのパラメータ\(λ\)、\(ψ\)を\(-\displaystyle\frac{π}{2} \leq λ \leq \displaystyle\frac{π}{2}\)、\(-π \leq ψ \leq π\)の範囲で動かしたときの終点をプロットすることで描ける曲面になるはずです。\(\boldsymbol{J}\)を\(λ\)、\(ψ\)と定数\(l_A\)、\(l_B\)、\(θ_A\)、\(θ_B\)を使って表すことがゴールとなります。
まずは、含余回転ジュエルベクトル\(\boldsymbol{j}\)について考えます。
\(\boldsymbol{j} = \displaystyle\frac{Δ(\boldsymbol{p}_A+\boldsymbol{p}_B)}{Δθ} = \boldsymbol{a} + \boldsymbol{b}\)
\(\boldsymbol{a} = \displaystyle\frac{Δ\boldsymbol{p}_A}{Δθ}\)
\(\boldsymbol{b} = \displaystyle\frac{Δ\boldsymbol{p}_B}{Δθ}\)
とします。
2025/10/16 追記&修正:
\(\boldsymbol{a}\)は\(x’z\)平面上の大きさ\(l_Ast\)のベクトル、\(\boldsymbol{b}\)は\(y’z\)平面上の大きさ\(l_Bs(1-t)\)のベクトルです。\(\boldsymbol{j}\)は\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の2つのベクトルの和になります。そして、\(\boldsymbol{j}\)は\(\boldsymbol{a}\)の向きを決定する\(φ_A\)、\(\boldsymbol{b}\)の向きを決定する\(φ_B\)、\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の大きさを決定する\(s\)、\(t\)によって変化することがわかります。\(j=J\)となるときは必ず\(s=1\)であるため、以降は\(s=1\)の場合で考えます。
\(\boldsymbol{a}\)は\(x’z\)平面上の大きさ\(l_At\)のベクトル、\(\boldsymbol{b}\)は\(y’z\)平面上の大きさ\(l_B(1-t)\)のベクトルです。\(\boldsymbol{j}\)は\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の2つのベクトルの和になります。そして、\(\boldsymbol{j}\)は\(\boldsymbol{a}\)の向きを決定する\(φ_A\)、\(\boldsymbol{b}\)の向きを決定する\(φ_B\)、\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の大きさを決定する\(t\)によって変化することがわかります。
\(\boldsymbol{e}_J(λ,ψ)\)を固定した場合に\(j\)および\(J\)がどのように決定されるかについて、詳しく考えます。\(\boldsymbol{a}\)または\(\boldsymbol{b}\)の向きが\(\boldsymbol{e}_J\)の向きと同じで、\(j\)が自明となる場合は省いた条件で考えます。\(\boldsymbol{a}\)、\(\boldsymbol{b}\)、\(\boldsymbol{e}_J\)について、以下のような関係が成り立ちます。
関係1: 始点を原点に揃えたときの\(\boldsymbol{a}\)、\(\boldsymbol{b}\)、\(\boldsymbol{e}_J\)の3つのベクトルは同一平面上にあり、\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の間に\(\boldsymbol{e}_J\)がある
関係2: \(\boldsymbol{a}\)と\(\boldsymbol{e}_J\)間の角度を\(α\)、\(\boldsymbol{b}\)と\(\boldsymbol{e}_J\)間の角度を\(β\)とすると、\(l_At \sin α = l_B(1-t) \sin β\)となる
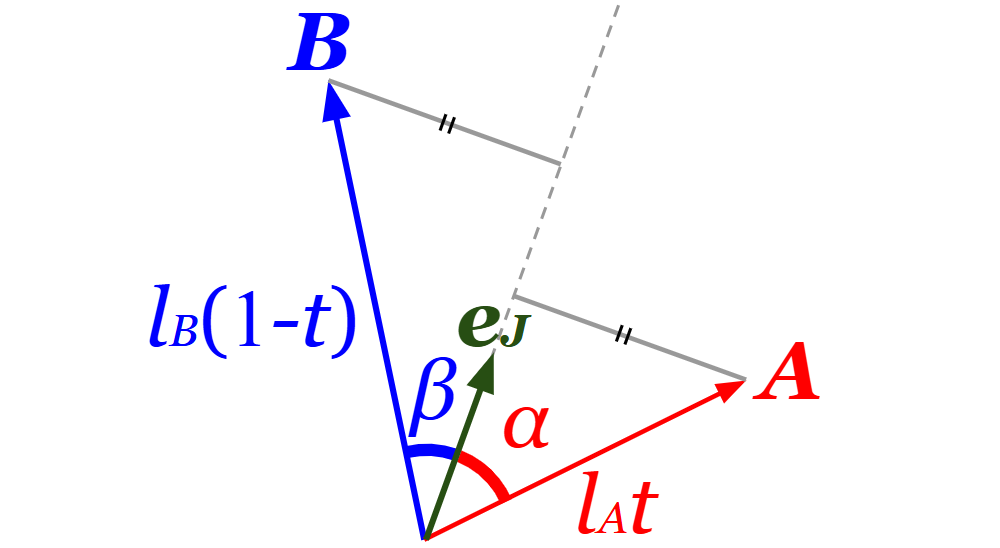
この関係を利用して\(j\)および\(J\)を求めます。まず、\(φ_A\)を決めると始点を原点に揃えたときの\(\boldsymbol{a}\)、\(\boldsymbol{e}_J\)が含まれる平面がつくられます。関係1より、この平面と\(y’z\)平面の交線の角度が\(φ_B\)になります。ただし、\(\boldsymbol{a}\)と\(\boldsymbol{b}\)の間に\(\boldsymbol{e}_J\)があるように\(φ_B\)を定めます。\(φ_B\)は\(φ_A\)、\(λ\)、\(ψ\)、定数によって表せるということです。
さらに、\(φ_A\)と\(φ_B\)が定まれば、関係2により\(t\)も定まります。つまり、\(φ_B\)と\(t\)はそれぞれ\(φ_A\)、\(λ\)、\(ψ\)、定数で表せ、\(j\)も\(φ_A\)、\(λ\)、\(ψ\)、定数で表せるということです。\(j\)が\(φ_A\)、\(λ\)、\(ψ\)、定数で表せるということは、\(j\)が最大になるとき(\(j=J\)になるとき)の\(φ_A\)がわかるということであり、そのときの\(φ_A\)は\(λ\)、\(ψ\)、定数で表せるはずです。\(j=J\)になるときの\(φ_A\)が\(λ\)、\(ψ\)、定数によって表せれば、ドミノ倒しのように\(φ_B\)、\(t\)、そして\(J\)を\(λ\)、\(ψ\)、定数によって表すことができます。
このような方法で、3次元の2セグメントジュエルの方程式が導けると考えています。ただ、もっと複雑な2セグメントを考えたときに、頑張って計算したことが無意味になるみたいなこともありそうなので、今無理に計算することでもないのかなと思っています。あと単純にもっとスマートな解法もありそうです。

ジュエルベクトルを用いた関係式
おまけの数式パートのラストです。
まず、ある時点でのセグメントAの角速度ベクトル\(\boldsymbol{\omega}_A \mathrm{\,[s^{-1}]}\)、セグメントBの角速度ベクトル\(\boldsymbol{\omega}_B \mathrm{\,[s^{-1}]}\)を使い、除余回転2セグメント角速度\(\tilde{\omega} \mathrm{\,[s^{-1}]}\)を以下のように定義します。
\(\tilde{\omega} = \displaystyle\frac{j}{J}(|\boldsymbol{\omega}_A|+|\boldsymbol{\omega}_B|)\)
・速度の関係式
セグメントB側の端のリンクの速度\(\boldsymbol{v} \mathrm{\,[m\,s^{-1}]}\)は、次のようになります。
\(\boldsymbol{v} = \tilde{\omega}\boldsymbol{J}\)
・パワーの関係式
2セグメントのパワーの入出力を表した関係式です。セグメントAに両リンクから加わるトルクベクトルの和\(\boldsymbol{\tau}_A \mathrm{\,[Nm]}\)、セグメントBに両リンクから加わるトルクベクトルの和\(\boldsymbol{\tau}_B \mathrm{\,[Nm]}\)、セグメントB側の端のリンクから外に加える力ベクトル\(\boldsymbol{F} \mathrm{\,[N]}\)を用いています。
\(\boldsymbol{\tau}_A \cdot \boldsymbol{\omega}_A + \boldsymbol{\tau}_B \cdot \boldsymbol{\omega}_B = \boldsymbol{F} \cdot \boldsymbol{v}\)
\(\boldsymbol{\tau}_A \cdot \boldsymbol{\omega}_A + \boldsymbol{\tau}_B \cdot \boldsymbol{\omega}_B = \tilde{\omega}\boldsymbol{J} \cdot \boldsymbol{F}\)
ここで、セグメントB側の端のリンクから外に加える\(\boldsymbol{e}_J\)方向の力\(F_J \mathrm{\,[N]}\)を次のように定義します。
\(F_J = \boldsymbol{e}_J \cdot \boldsymbol{F} = \displaystyle\frac{\boldsymbol{J} \cdot \boldsymbol{F}}{J}\)
\(F_J\)を用いるとパワーの関係式を次のように変形できます。
\(\boldsymbol{\tau}_A \cdot \boldsymbol{\omega}_A + \boldsymbol{\tau}_B \cdot \boldsymbol{\omega}_B = \tilde{\omega}JF_J\)
\(\displaystyle\frac{ \boldsymbol{\tau}_A \cdot \boldsymbol{\omega}_A + \boldsymbol{\tau}_B \cdot \boldsymbol{\omega}_B }{\tilde{\omega}} = JF_J\)
これは、2セグメントへのパワーの入力全体、除余回転2セグメント角速度(パワーの入力に貢献する角速度)、ジュエルベクトルの大きさ、セグメントB側の端のリンクから外に加える\(\boldsymbol{e}_J\)方向の力(パワーの出力に貢献する力)の関係を示しています。簡単に言えば、2セグメントの変速機としての機能を示しているということです。
説明をわかりやすくするために、数式パート以外では大きく間違ってはいないものの多少間違った表現もしました。しかし、最後に示した数式がすべてです。この数式から導けることが正しいです。

運動効率の研究の第1章は終わり
2セグメントジュエルで示される変速機としての2セグメントを介して、筋肉のパワー発揮特性と運動の目的に合ったパワー発揮をざっくりと結びつけたところで、身体運動の効率に関する研究の第1章は終わりました。ざっくりと運動の効率を決定する主要なものは何かをつきとめられたということです。
この第1章が一番見通しが立たなくて、努力でどうにもならないところでした。がんばった分だけできるようになる勉強とは違って、ある種の天才性であるとか、ひらめきであるとか、そういう不確実な運の要素が大きかったです。この第1章を今の時点で終えられたのは、かなり運が良いと言えますね。一生終えられないってことも最悪あったと思うので。

第2章の課題のすべて
さあ、ここから身体運動の効率に関する研究の第2章の始まりです。第2章は細かいところを詰めていきます。何から手をつけていいかわからなかった第1章とは違って、第2章では課題は明確です。課題は以下の5つに大別できます。
① 質量、慣性モーメント、重力、運動エネルギー、位置エネルギーがある場合への拡張
② 筋腱のつき方(発揮するトルクの指向性、モーメントアーム)、量、筋線維の角度、筋線維のパワー発揮特性等を考慮した場合に何が起きるか考える。2セグメントジュエルの変形?
③ 複数の2セグメントの連動
④ 連続的な変化を考える。ある点での効率ではなく、ある経路での効等率を考える。積分する感じ。
⑤ 単純な2セグメントよりも複雑な機構の場合
(⑥3次元の2セグメントジュエルの方程式の完成
解く順番はないと思います。むしろこれらを同時並行でやることで、お互いがお互いをほぐしあって解けるのではないかと考えています。

第3章で相馬眼の新理論が完成する
第2章が終われば、起こった運動の効率が解析でき、また一から効率の良い運動を起こすことまでできるはずです。おそらくそれが第3章になるんだと思います。
第3章で、ようやく実践的な、具体的な運動を扱います。どうしたら速く走れるか、強いパンチを打てるか、球を速く投げられるか、他。運動の目的と制約を考え、どのような体をつくり、どのように個々の筋肉を制御するか、というのがテーマになってきます。第3章は以下の3つの分野に大別できるはずです。
① 目的、制約、効率の評価、その詳細
② 効率の縦の比較。ある体が用意されたときに、それをどのように動かせば最も効率がよくなるか
③ 効率の横の比較。複数の体それぞれが最も効率よく動くとき、どの体が最も効率がよくなるか
③はこれつまり、「相馬眼」です。相馬眼が、ようやく数式によって表される厳密な世界へと移るのです! これはすごいことです! 響いてください。




