「身体運動の効率を完璧に理解したい！」
私は心の底から思っています。

運動の効率がほぼ完璧に理解できれば、ウサインボルトがなぜ速く走れるのか、井上尚弥がなぜ速く強いパンチを打てるのか、逆にダメな人はどこを改善したら良いのか、そういうことが明確に説明できるようになるはずです。

あらゆる運動の効率がたった1つの普遍的な理論で説明でき、ちょっとした発想の転換による少ない計算・理解コストでコーチングなどの現場に還元可能な、そういうものをつくりたいんです。ただ、今バイオメカニクス界に流通している道具では無理です。新しい発想をしなければいけないんです。

私のこれまでの経験と直感から、運動の効率の理論がそこそこの完成系になるまでに、私の力だと2年くらいはかかると思っていました。そして、今が研究を始めてからだいたい6ヵ月です。6ヶ月/2年にしては中々よい進捗状況だと思っています。

一体どこまで研究が進んだのか、残っている課題はなんなのか、今回はその中間発表を行いたいと思います！

いろいろ発表していく前に、キャッチーなカッコいいワードを含んだ現時点でのまとめ的な文を置いておきます。

運動の効率は「リンク経路」を見ればわかり、「リンク経路が直線」になるように筋肉を鍛えたり神経を磨くことで、速く走れたり強いパンチが打てたりと良い動きができるようになる。

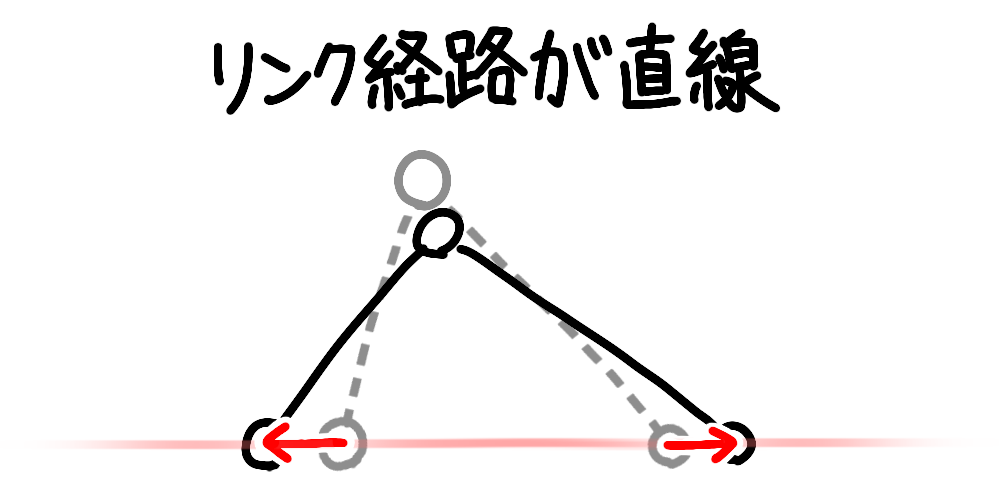
まあ、仮説なんで全然的外れなことを言ってる可能性はありますが。ちなみに冒頭で名前を出した井上尚弥は「リンク経路を直線に動かす能力」に優れ、非常に高精度な効率の良い運動を常時行っているボクサーであると私は見ています。

運動の効率と言っても、その定義がどうのだとか、そもそも前提となる条件がどうのだとか、運動の効率の中での分類をどうするだとか、細かいことを気にし出すと中々攻め込めません。

なので私はもういきなりド本丸から攻めてしまっています。ざっくりとした運動の効率の本質・原理を理解することが先で、細かいことは後から考えるのです。

というわけで、これから言うことはかなりざっくりしています。論理展開もざっくりしています。ざっくりなので正確ではない表現もします。ざっくり解説です。

まず、効率ってなんでしょうか。そこから考えたいと思います。

ただまあこれは普通に考えてエネルギー効率のことでしょう。筋肉を動かすのに投入したエネルギーが、どれだけ運動の目的に結びつくエネルギーに変換されて、どれだけのエネルギーがロスになるか、ということです。

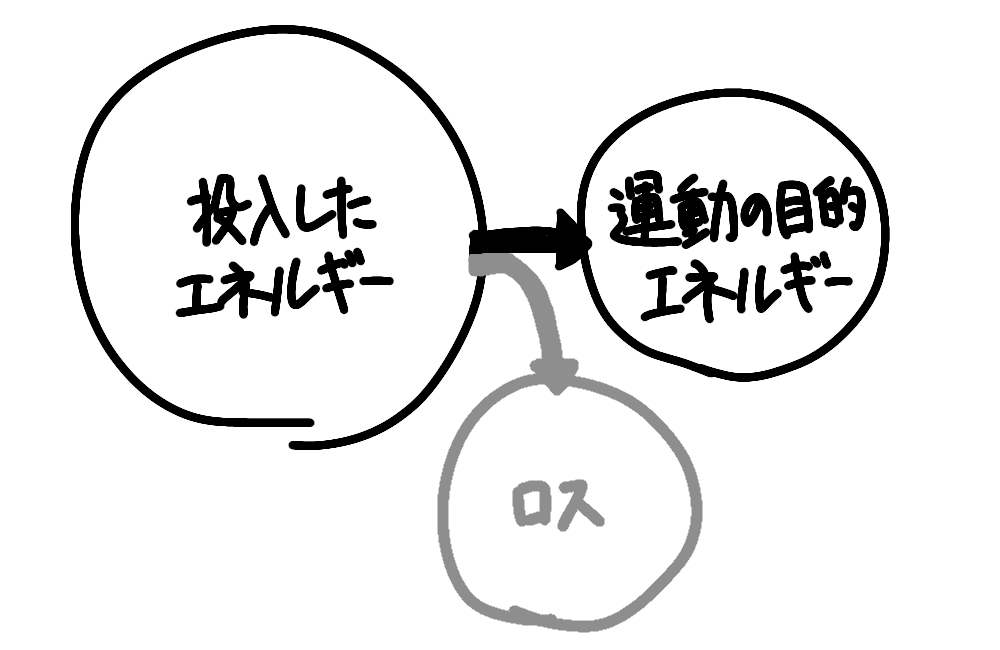
運動の目的に結びつくエネルギーは、球を投げる場合なら球の運動エネルギー、走る場合ならその人の重心の並進運動エネルギー、特殊なところでは弓を引くときの弓の弾性エネルギーとかです。まあ深く考える必要はありません。本質ではないので。

エネルギーのロスをなくすことは、単に少ないエネルギーで目的の運動ができるようになるだけでなく、MAXのエネルギーを使ったときにより強い運動（運動の目的に結びつくエネルギーが強くなる）ができるようになります。とにかくエネルギーのロスをなくしたいんです。

運動の中でも走っているときのエネルギーの遷移を考えます。まず、走っているときにエネルギーの投入がないと、空気抵抗や地面との摩擦、体の中の摩擦で止まってしまうということはハッキリさせておきます。これはそういうもんです。走るためにはエネルギーの投入が必要なんです。あと摩擦は熱エネルギーを生み出します。摩擦熱ってやつですね。

ここからは少し専門知識が必要ですが、運動するときのエネルギーを分類すると、（筋肉を働かせるための）化学エネルギー、運動エネルギー、重力位置エネルギー、弾性エネルギー、熱エネルギーに分類できます。

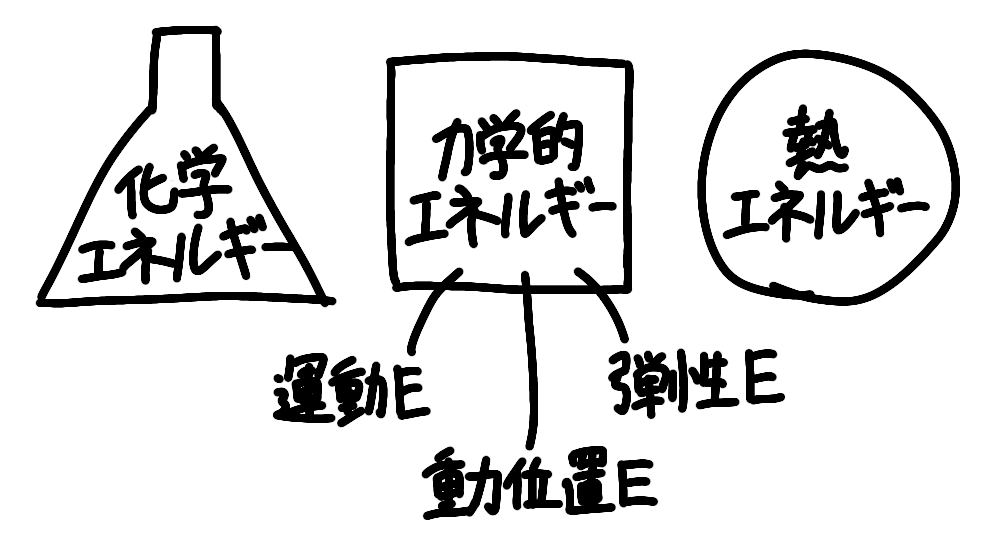
運動エネルギー、重力位置エネルギー、弾性エネルギーはそれぞれ可換なので区別する必要はないとして力学的エネルギーにまとめてしまいます。そうすると、化学エネルギー、力学的エネルギー、熱エネルギーになります。まあ、そうなるんです。

そして、エネルギーの流れは方向があります。
　化学エネルギー　→　力学的エネルギー　+　熱エネルギー
　力学的エネルギー　→　力学的エネルギー　+　熱エネルギー
といった具合に。

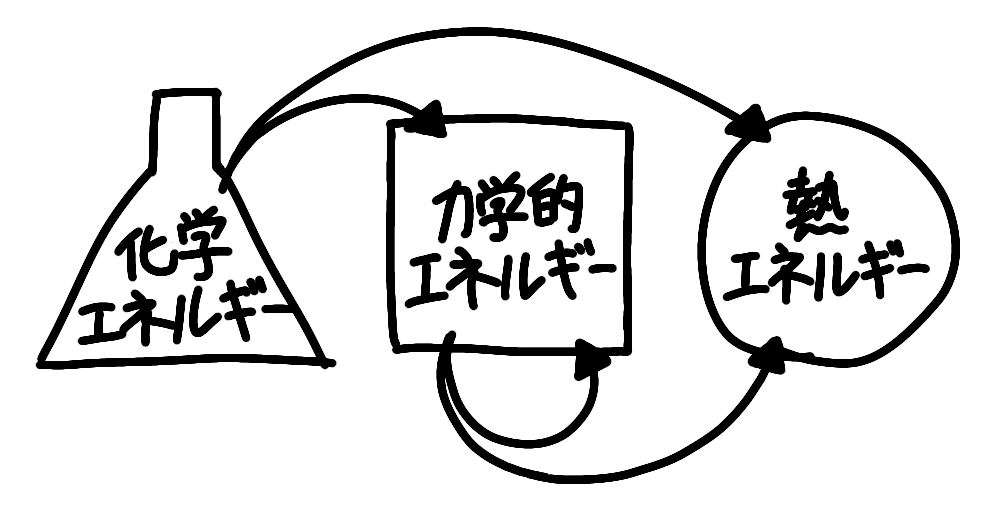
で、熱エネルギーになったらおしまいです。熱エネルギーを力学的エネルギーや化学エネルギーにできる人はいません。サウナに行っても、サウナの熱を吸収して体を動かすおっさんや、サウナの熱を吸収してエネルギーを補充するおっさんはいませんよね。

あとは、運動の目的に結びつくエネルギーに変換できない、利用できない力学的エネルギーもロスになります。

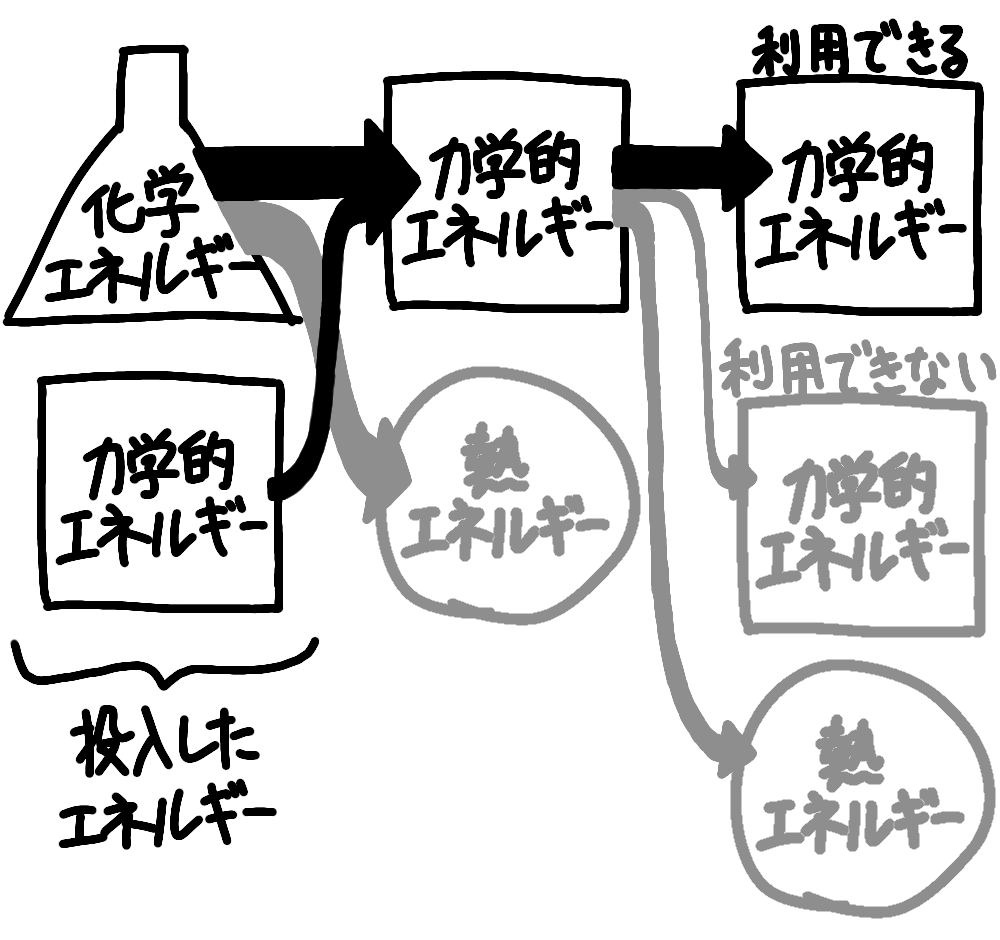
空気抵抗があるのは空気に熱エネルギーと運動エネルギーを与えているからで、その空気の運動エネルギーは走るための力学的エネルギーには変換できないので、空気に与えた運動エネルギーはロスになります。（熱エネルギーを運動のエネルギーと捉えれば、運動の目的に結びつくエネルギーに変換できない力学的エネルギーの中に熱エネルギーが含まれているんですけどね。）

このパートの結論は、「エネルギーをロスしないのがいい」です。細かいことはわからなくても、これさえ押さえておけば大丈夫です。

エネルギーのロスにはいろいろな種類がありますが、ここでごっそりそぎ落とします。本質ど真ん中以外のエネルギーのロスは一旦考えないことにします。まず私が調べたいのは筋肉とか骨格とか、そういう感じの体の中で生まれるロス、体の中で生まれる熱エネルギーなんです。この時点で空気抵抗は除外されますね。

さらに、体の中では体の中での摩擦で熱エネルギーが発生しますが、そのメイン、本質ど真ん中となるのは筋肉の中で発生する熱、筋肉の中での摩擦です。ここは所説ありですが、まあ普通に考えたらそうなんじゃないでしょうか。
（他の原因の比率が大きくても、それがメインになることはないと思うんですね。例えば、脂肪がたぷんたぷんすることで生じる摩擦とかも結構影響ありそうですが、それってメインではないというか、空気抵抗と同類の、あくまで付随要素な感じがするんです。）

筋肉の中での摩擦とは、筋肉の粘性のことです。筋肉の中で筋肉の粘性によって力学的エネルギーが熱エネルギーに変わります。まあ、摩擦熱と同じことです。筋肉の中で擦れて熱が発生します。

力学的エネルギーをなるべく熱エネルギーにしないためには、筋肉の粘性をなるべく使わないようにすることが求められます。

このパートの結論は、「エネルギーをロスしないために、筋肉の粘性を使わないのがいい」です。

あっ、粘性が絶対悪みたいに言いましたが、高い場所から飛び降りて着地するときなどエネルギーを吸収したい（なるべく力学的エネルギーを熱エネルギーにしたい）ときは、なるべく筋肉の粘性を使った方がいい、のようなことがあると思っています。粘性もヒーローになれるはずです。

粘性を使わないためにはどうしたらいいかを考えます。結論、粘性を考えると「速い動きは悪」になります。

ペンキみたいなドロドロした粘度が高い液体を棒でかき混ぜることを想像します。シンプルに1周だけかき混ぜるとします。

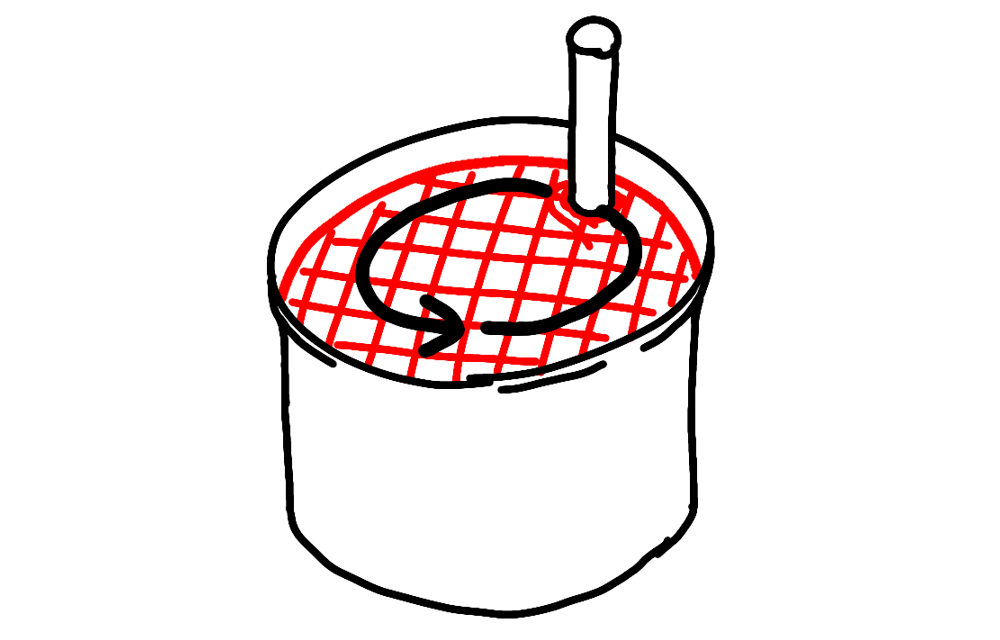
この1周かき混ぜのとき、速くかき混ぜるほどかき混ぜるのに大きな力が必要となり、結果的に多くのエネルギーが必要となります。まあそういうもんなんです。そしてそのエネルギーは最終的にペンキの熱エネルギーになります。
イメージとしては、速い動きをするほど、摩擦でブレーキがかかるのと同じように粘性でブレーキがかかって、摩擦熱と同じようにエネルギーが熱エネルギーになっちゃうってことです。

筋肉でも同じようなことが行われると想像できます。ざっくりとしていますが、筋肉（筋腱）が速く伸び縮みするほど粘性でブレーキがかかってしまい、力学的エネルギーが熱エネルギーになってしまうと考えています。

ここでパワーについて考えます。パワーはエネルギーと密接に関わっています。というかエネルギーを秒数で割っただけのものがパワーです。ほぼエネルギーです。

そんなパワーですが、簡単に表すと「パワー=力×速さ」です。「速さ」が出てきます。

筋肉がパワーを発揮するときを考えます。同じパワー（パワー=力×速さ）でも「力」が大きく「速さ」が小さい場合と、「力」が小さく「速さ」が大きい場合がありますが、どちらがエネルギーのロスを少なくできるでしょうか。粘性を考えると「速い動きは力学的エネルギーを熱エネルギーに変換する悪」であることから、できるだけ「力」を大きく「速さ」を小さくしてパワーを発揮するのがいいとなります。

このパートの結論は、「エネルギーをロスしないために、筋肉の粘性を使わないために、筋肉は力を大きく速さを小さくしてパワーを発揮するのがいいのでは」です。

かなりざっくりとした論理展開だったので、こぼしていることが多くあると思います。しっかりとやるなら筋肉（筋腱）のある程度正確なモデルを作って計算することが必要になってきますね。ただこれ、モデルも計算も実は結構複雑な処理が必要になるんじゃないかと思っています。
少し専門的になりますが、今のところ私が考えて支持している筋肉の簡単なモデルを紹介します。バイオメカニクス界でよく使われる、要素が全部並列のものではなく、並列直接合わさったものになってます。並列直接合わさったものの方が生物としてより安全で合理的な設計というか、組織のふるまい的によりあり得そうというか、そんな感じがするんですよね。完全な直感で、ちゃんと検証していませんが。

一旦筋肉から離れて、リンクセグメントモデルについて見ていきます。

リンクセグメントモデルとは、人間や動物を非常に単純化して捉えたモデルです。単純化された人や動物には意思も尊厳もありません。あるのは「リンク」と「セグメント」だけです。非常に恐ろしいですね。

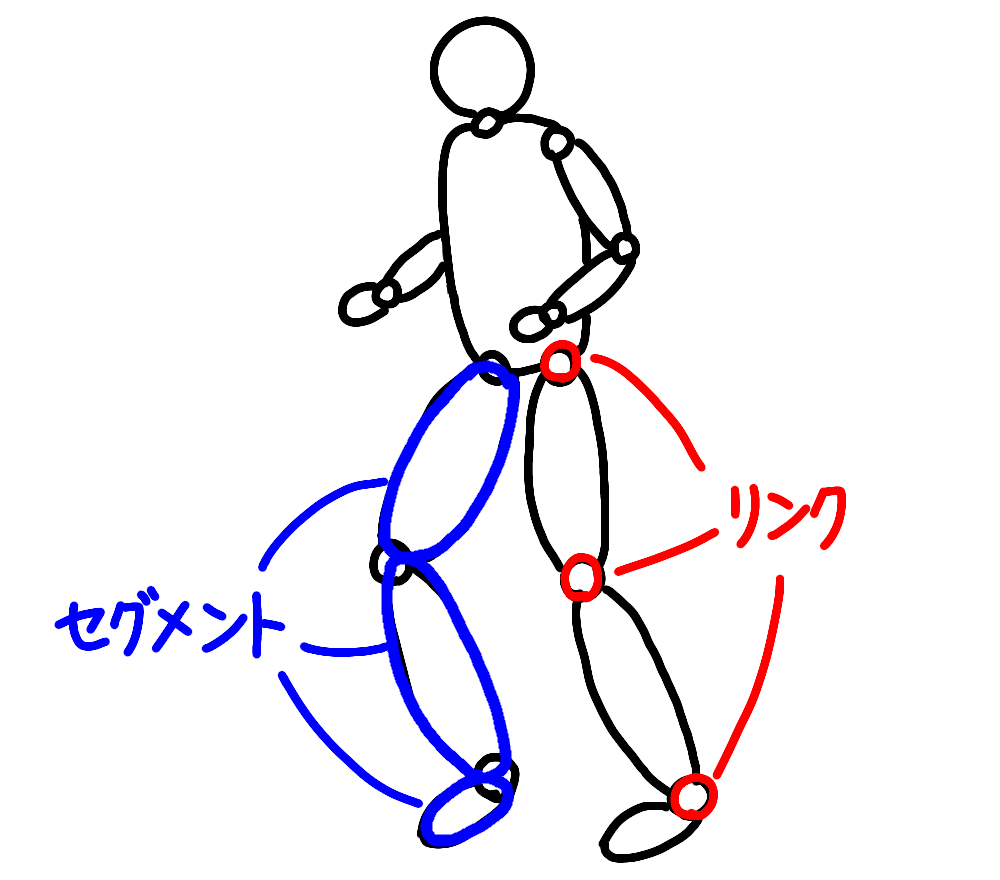
リンク=関節、セグメント=骨と骨に引っ付いてる血肉、みたいな感じです。脚なら膝関節・足首関節がリンクで、大腿部・下腿部・足部がセグメントです。

スポーツ分野のバイオメカニクスでは、このリンクセグメントモデルをバリバリ使います。このセグメントの加速度があーで、この関節にかかる力がこーで、角加速度がー、関節トルクがー、のような呪文を唱えながら、大変な計算をするわけです。

さて、このリンクセグメントモデルなどで体の動きを見るだけで、運動の効率はわかるのだろうか、それも計算しまくりではなく簡単なコツを用いて、ということを考えます。

普通の人や計算から入る人は、無理だと思う人が多いと思います。リンクセグメントモデルなど体の動きを見るときに扱う表に出てくる変位や力という量が、裏で隠れているエネルギー効率という量とは違う場所にいるように見えるからです。

ただ、私のように観察と感覚から入る人は、良くも悪くもそこをすっ飛ばすことができます。あっ効率の良い動きと効率の悪い動きってなんかわかるなあ、わかるってことはなんか違うんだろうなあ、具体的にはわからないけど確かになんか違いはあるぞ、という感覚がまずあってそれが研究課題になるので、わかるかどうかではなく、わかるという確信から入ることができるのです。ありがたいことに。

そしてさらなる観察と感覚から、たくさんあるセグメント全体を見るのではなく、2セグメントの塊に分けて、それぞれの2セグメントに注目すればいいんじゃないかと思うようになりました。

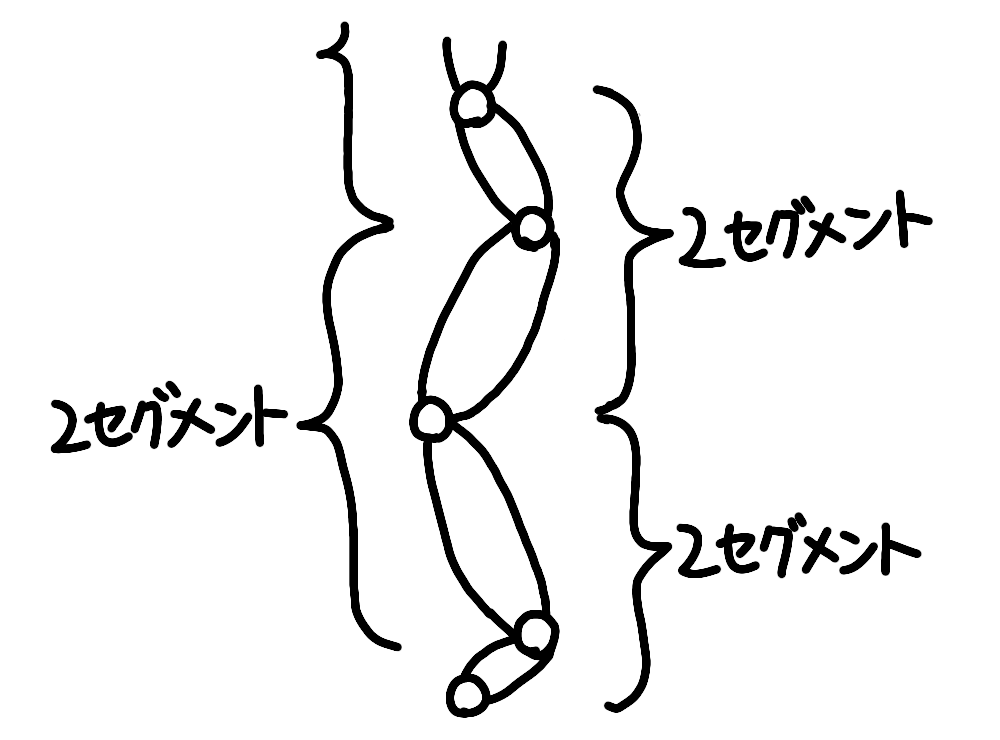
ここに来るまでにエネルギーだとか筋肉の粘性だとかいろいろ話をしましたが、実はそこが思考の出発点ではなく、出発点はこの2セグメントに注目すればいいのではという感覚です。正直言ってあとは理由付けの作業なのです。

このパートの結論は、「なんか知らんけど2セグメントに注目したらいいんじゃね？」です。

このパートは丁寧な解説なしで少し難しい話をします。難しいと感じた場合はこのパートの結論まで飛ばしてしまっても問題ないです。実は私自身もよくわかっていないのが難しいに輪をかけてちゃっているんですよね。すみません。

まずは、2セグメントを超シンプルな現実ではありえないものにしてしまいます。あくまで本質を考えたいので、シンプルに。

・それぞれのセグメントの両端がリンク
・それぞれのセグメントの両端にしか外から力・トルクは加わらない（両端でしか外に力・トルクは加えられない）
・それぞれのセグメントは変形しない
・それぞれのセグメントの質量は0
・それぞれのセグメントは初期状態で静止している

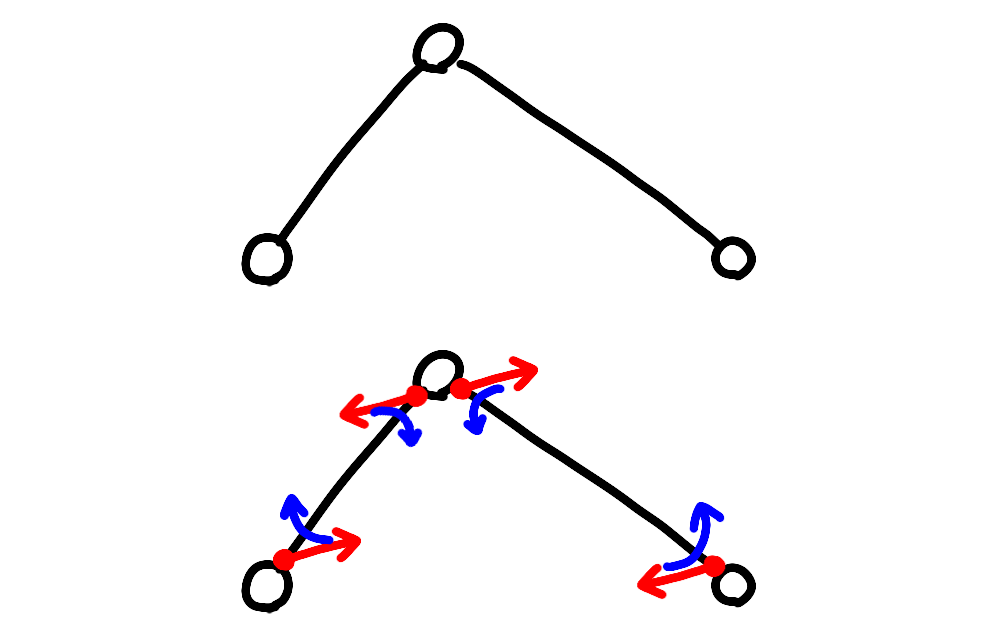
2セグメントの内と外とで考えると、2セグメントに加わる外力となる力・トルクは2セグメントの両端のリンクにのみ加わります。さらに質量が0なことから、2セグメントおよびそれぞれのセグメントについて、外力となる力とトルクは釣り合うことになります。

質量0というのは実際にはありえない無茶苦茶な仮定ですが、質量に対してかなり大きな力が加わる場合と似ている状況なのではないかと思います。まあ、加速度・慣性力・運動エネルギー・重力位置エネルギーなどなど面倒なことを考えたくないってのが一番の理由です。

次に、2セグメントの機構、2セグメントの役割について考えます。

2セグメントは、2セグメントの間の角度が変化すると、2セグメントの長さ（2セグメントの両端の距離）が変化します。

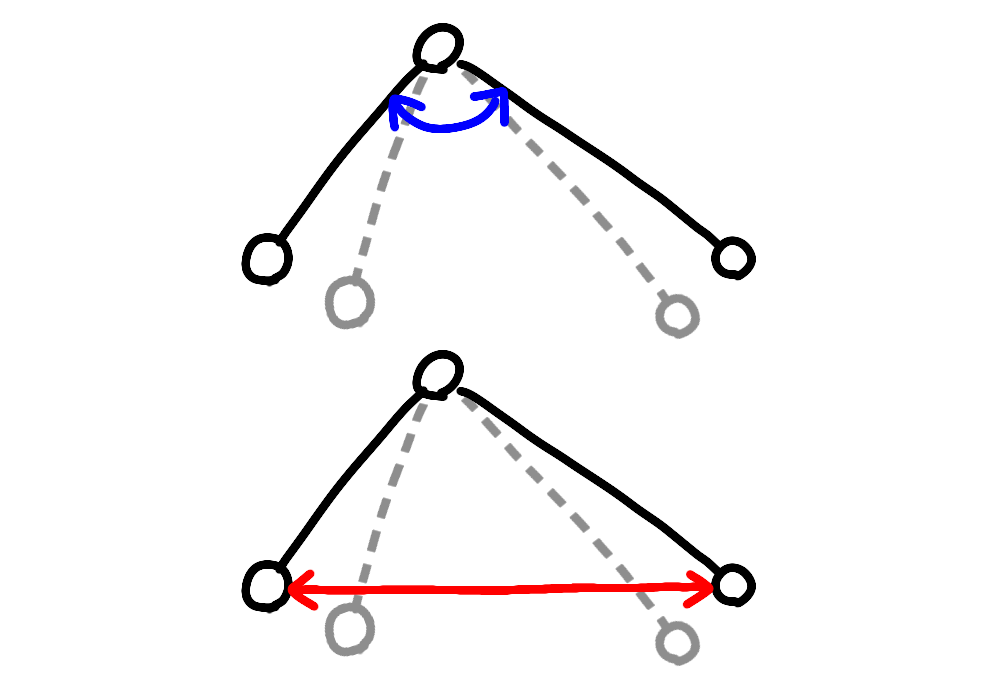
この角度と長さの変換が2セグメントの役割だと私は考えています。これを発展させて考えると、「トルク・角度」の仕事と「力・距離」の仕事の変換、「トルク・角速度」のパワーと「力・速度」のパワーの変換、これらも2セグメントの役割だと考えることができます。たぶん。

ここからさらになんとなくの話をします。

同じパワーではありますが、「トルク・角速度」のパワーを「トルクパワー」、「力・速度」のパワーを「力パワー」と表現して区別したいと思います。で、勝手にトルクパワー側を入力、力パワー側を出力のイメージで考えたいと思います。

2セグメントにおけるトルクパワーの入力は、端のリンク（外から加わるトルクベクトル・そのリンクに接するセグメントの角速度ベクトル）×2 +間の1リンク（間のリンクのトルクベクトル・2セグメント間の角度の角速度ベクトル）の3点、力パワーの出力は端のリンク（外に加える力ベクトル・そのリンクの速度ベクトル）×2の2点になります。

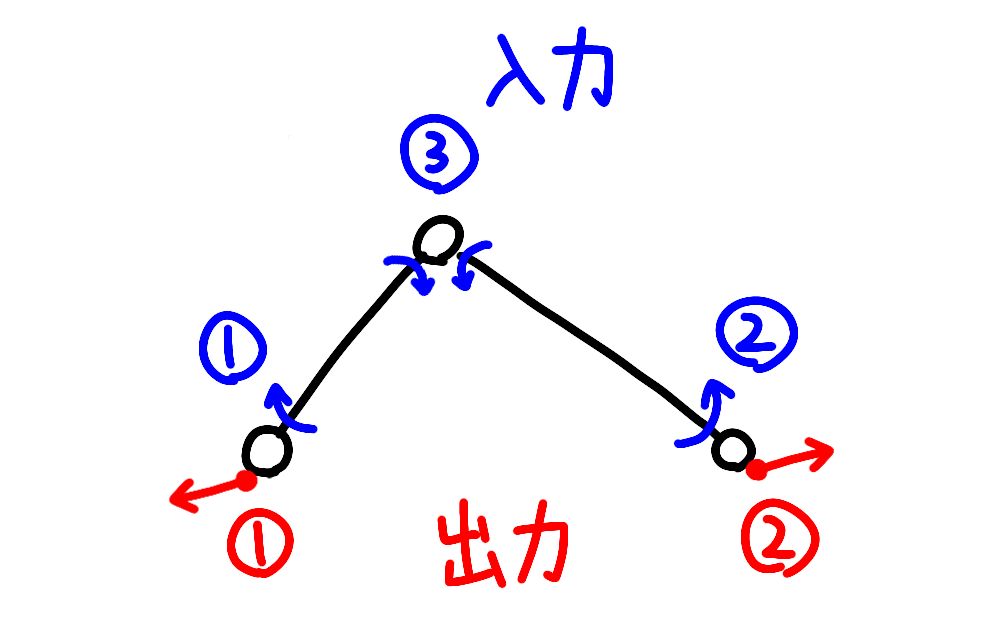
このとき、パワーの入力と出力は同じになるはずです。また、パワーはプラスのパワーだけではなく、マイナスのパワーもあります。当然マイナスの入力、マイナスの出力もあり、入力がマイナスになれば出力もマイナスになります。

ちなみに、2セグメントの間の角度が変わらない場合は、それは1セグメントとみなすべきで、さらに隣のセグメントと2セグメントを作る必要があると考えています。

まあ、細かいことは置いておいて、とにかく2セグメントのパワー発揮を考えると答えに近づけるような気がするんです。だってなんとなく筋肉のパワー発揮と結びつきそうじゃないですか？

そして、具体的にどこがどうなればいいのかはわかりませんが、なんとなく2セグメントも筋肉と同じように、力を大きく速さを小さくしてパワーを発揮するのがよさそうじゃないですか？

このパートの結論は、「エネルギーをロスしないために、筋肉の粘性を使わないために、筋肉が力を大きく速さを小さくしてパワーを発揮するために、なんか2セグメントも力を大きく速さを小さくしてパワーを発揮するのがいいんじゃね？」です。

2セグメントの両端のリンクが移動するときの経路を「リンク経路」と呼ぶことにします。真ん中のリンクは考えなくて大丈夫です。

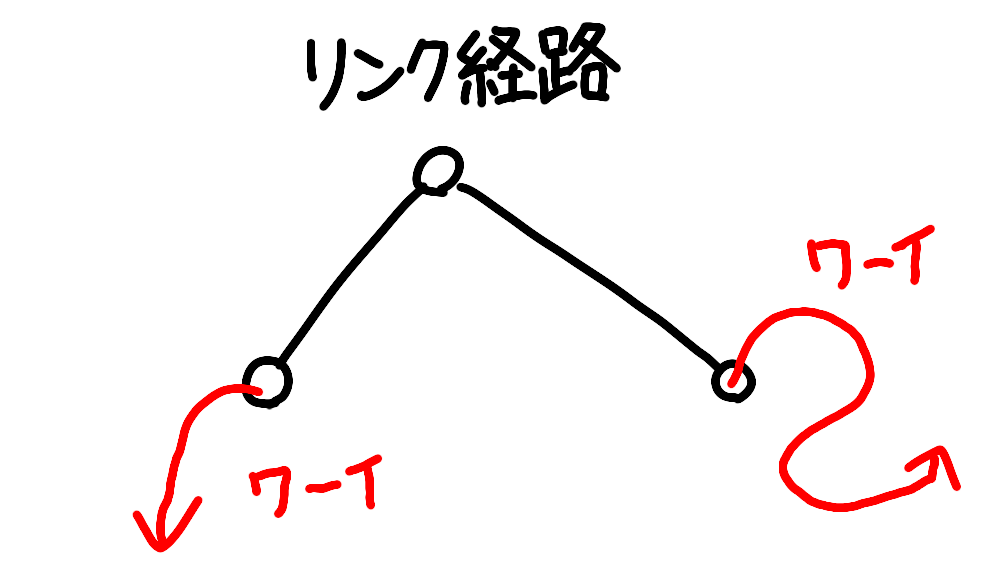
そして、2セグメントの両端のリンクが、移動前の両端のリンクを通る直線上を動くことを「リンク経路が直線」と表現したいと思います。

結論から言うと、「リンク経路が直線だと運動の効率が最もよくなるのではないか」と考えています。

最もよくなると言うからには、直線だと「何か」が最大もしくは最小になる、そういう美しい法則があるはずです。そして最大もしくは最小になる「何か」の有力な候補を1つ見つけました。それは経路の長さです。

2セグメント間の角度がある一定の量変化したとき、2セグメントの両端のうちの1つのリンクから見た、もう1つのリンクが移動する経路の長さは、リンク経路が直線のときに最も短くなります。

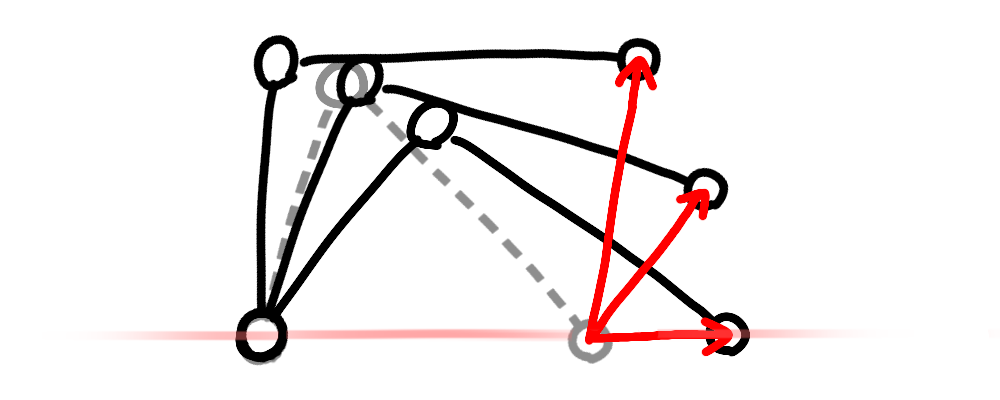
それ以外のことは全くわかっていませんが、なんとなく力を大きく速さを小さくしてパワーを発揮することと結びついていそうじゃないですか？　長さを時間で割ったら速さですからね。

この経路が最短になることが直接本質に結びついているかどうかはわかりませんが、とにかくリンク経路が直線かということは本質とガチガチにくっついていると思っています。

あとは、同じ経路を同じ時間内に両端のリンクが移動する場合でも、リンクが移動する速度的なもの？が一定なほど効率がよくなる気がします。これも速度的なものが具体的に何なのか、そもそも本当にそんなことがあるのか、全くわかっていませんが、なんとなく速いところと遅いところがあるとダメな気がします。

この中間発表の結論は、「エネルギーをロスしないために、筋肉の粘性を使わないために、筋肉が力を大きく速さを小さくしてパワーを発揮するために、なんか2セグメントが力を大きく速さを小さくしてパワーを発揮すればよさそうで、そのためになんかリンク経路は直線かつなんかリンク移動の速度的なものが一定？がいいんじゃね？」です。

これが今の私の到達点です。今の私の精一杯です。

「リンク経路が直線だといい」ということは、自分の体を使って簡単に体感することができます。

みなさん、ストレートパンチで誰か、もしくは何か、もしくは空気を殴ってみましょう。上腕と前腕の2セグメントを意識します。

①上腕と前腕の2セグメントのリンク経路が直線になるようにいいタイミングで腕を伸ばす場合
②前腕を先に出して上腕を後から出す（肘関節を先に伸ばして肩関節を後から伸ばす）場合
③上腕を先に出して前腕を後から出す（肩関節を先に伸ばして肘関節を後から伸ばす）場合

どれが一番力強いパンチを打てるか、ぜひ体感してみてください。

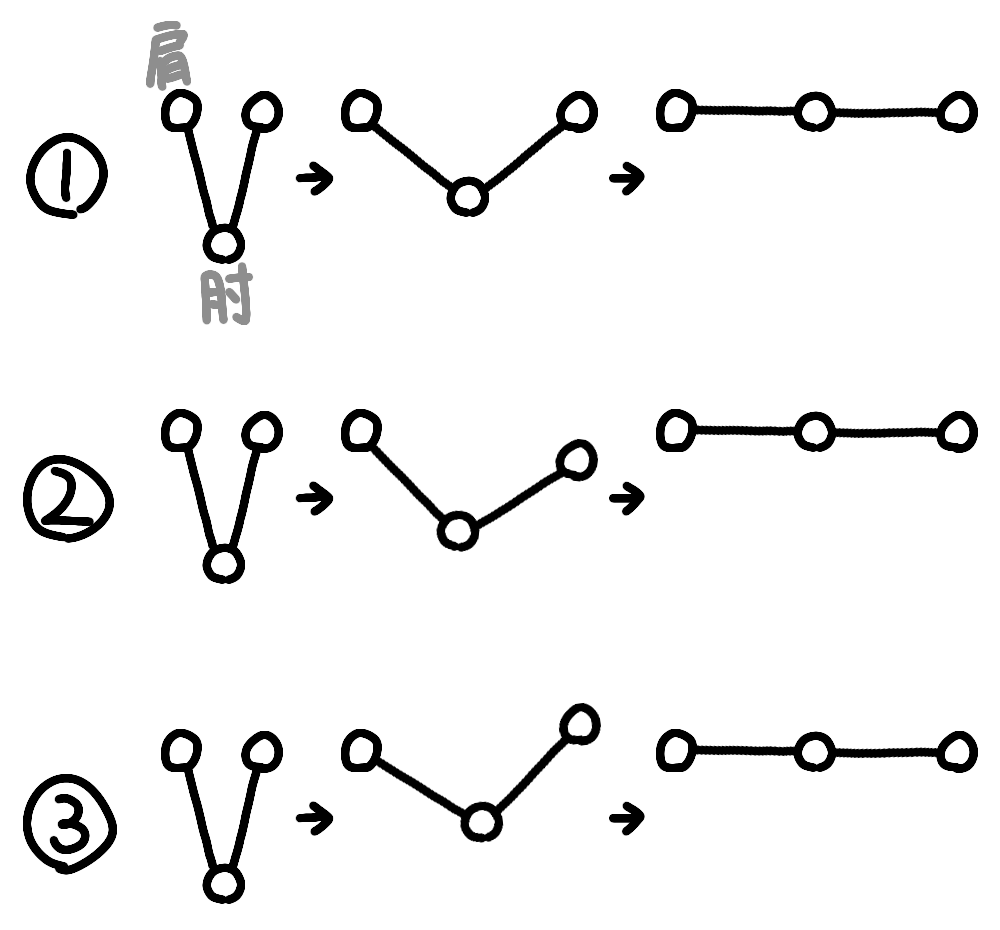
おそらく、①が一番力強いパンチを打てるはずです。少なくとも私はそうでした。

あとは、2セグメントのふるまいをもっと深堀りして、さらに2セグメントのふるまいと筋肉のパワー発揮との関係を結び付ければ、運動の効率の原理をざっくりと説明できるようになると考えています。

ただ、これが意外に難しんですよね。あと2,3アイデアでコロッと簡単にいけそうにも思うんですけど、私の頭では結構時間がかかってしまいそうです。本当にちょっとしたアイデアを思いつくかどうかだと思うんですけどね。

頭をやわらかくしないとですね。頭がやわらかくなる水を飲んでおきます。ちょっとお高い水なんですけど。

え？　怪しい？

ショウさんっていう絶対信頼できる人から買ったから大丈夫ですよ。感覚的に絶対大丈夫です！　私の感覚は絶対ですから！