走っているときのスタンス期の割合や、地面から加わる力が解析できるモデルの提案。ドーピング検知への応用も。
contents
- ドーピングの有無を見分けるために構築しました
- 状況が変化しない理想の1完歩について
- 座標系の設定
- 滑走時垂直抗力\(N\)の定義
- 特殊な平均の力の図
- 能動的な力
- 走能力数\(A\)の変化
- 受動的な力
- 特殊な平均の力と地面から見た理想の1完歩での平均加速度
- 特殊な平均の力とスタンス期の割合
- 早期負重度\(s\)
- 正の値をとる力の力積
- \(F_{pw}\text{-}A\)グラフ
- 偽速度\(d\)の導入
- 偽速度\(d\)の幾何学的理解
- 偽速度\(d\)と\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)の関係についての予想
- \(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)と後肢負重率
- 地面の変化による加速度補正数\(C\)の変化
- ドーピングの有無の見分け方についての予想
- ドーピングをしている走りの例
- 歩きについて
- 疲れました
※2025/6/25 更新
2025/6/25 追記:下に書かれているモデルの、修正版&清書版となる論文(査読前)のPDFを私のサイトに載せました。興味のあるご変態のお方はこちらからどうぞ。
(あっ、つまり下に書かれているモデルはちょい古いということです。ただ、超重要なメインの主張である「疲労しにくくなる系のドーピングをしている人や馬は、スパート中のスタンス期中の負重時期(早期負重度)があまり変化しない」というのは変わっていません。)

ドーピングの有無を見分けるために構築しました
私は人や馬の走りから、ドーピングをしているかどうかがわかります。と、宇宙と交信してそうなヤバそうなことを言いましたけど、ヤバくない人間です。ちゃんとした見分け方を基にちゃんと見分けられます。
その見分け方とは、疲労しにくくなる系のドーピングをしている人や馬は、スパート中のスタンス期中の負重時期(早期負重度)があまり変化しない、というものです。
スパート中は段々とスタンス期の早い時期により負重するようになるのですが、疲労しにくくなる系のドーピングをしているとこの変化が極端に小さくなるんです。(…うーん。ヤバさのベクトルが変わっただけな気がしますが。)
これもただテキトーに言っているわけではありません。元々そうだということは3, 4ヵ月前からわかっていたのですが、それだけでは弱いので、どういう原理や計算式でそうなるのかまで考えました。そして構築したのが今回紹介する「特殊な平均の力モデル」と「偽速度モデル」なわけです。
特殊な平均の力とか偽速度ってのは、自分だけで考えるときに自分だけに伝わればいいよね的なノリで使っていた用語で、今もそれをズルズルと引きずっています。なので、モデルの名前は仮です。もっとカッコいい名前があればそれにします!
さて、私はこのあと「〇〇〇はドーピングをしていた!!」のような記事を書きます。で、そのときに何テキトーなことぬかしてやがるんだと言われないための根拠を書いておく、というのが今回の目的です。とりあえず根拠がこれですよと示したいだけなので、人に説明する用に書いていません。わかりやすさ0です。一部の特殊な人間を除いて読み進めるのは難しいでしょうし、基本読まなくていいです。
まあこのモデルから導かれる結論には、ドーピングの有無の見分け方以外にも重要なものがめちゃくちゃあるので、のちのち「5.解析編」みたいなのを作って、そこでわかりやすく説明できたらいいなと思っています!
ではさっそく、わかりやすさ0で説明していきます。

状況が変化しない理想の1完歩について
このモデルでは、「状況が変化しない理想の1完歩」を基本として考える。縮めて「理想の1完歩」と呼ぶこともある。
走行中の速度や加速度、肢に加わる力などは、1完歩の中で変化する。レース全体での速度や加速度、肢に加わる力の変化など、比較的マクロな変化を扱う場合は、1完歩での平均の値を扱いたい。
だたし実際の1完歩では、1完歩中でも状況は常に変化している。具体的に言い換えると、1完歩中のある時点\(t\)を中心とした1完歩の平均の速度や加速度などの状況\(\boldsymbol{X}(t)\)が、\(t\)によって変化している、ということである。
この1完歩では、理論上で本当に扱いたい値である、状況を固定したときの1完歩での平均の値は導き出せない。
対して、1完歩中のあらゆる時点\(t\)でも\(\boldsymbol{X}(t)\)が変わらない1完歩のことを、状況が変化しない理想の1完歩と呼ぶ。
状況が変化しない理想の1完歩は実際には存在しないが、これを考えることで、状況を固定したときの1完歩での平均の値が扱えるようになり、理論上で処理がしやすくなる。

座標系の設定
右手直行座標系を用いる。
身体重心を原点とする。
地面を平面とし、その平面に垂直上向きになるように\(z\)軸をとる。
進行方向(地面から見た理想の1完歩での平均速度\(\boldsymbol{v}_u\)の向き)に\(x\)軸をとる。\(x\)軸は\(z\)軸に直行する。
右手直行座標系になるように\(y\)軸を取る。
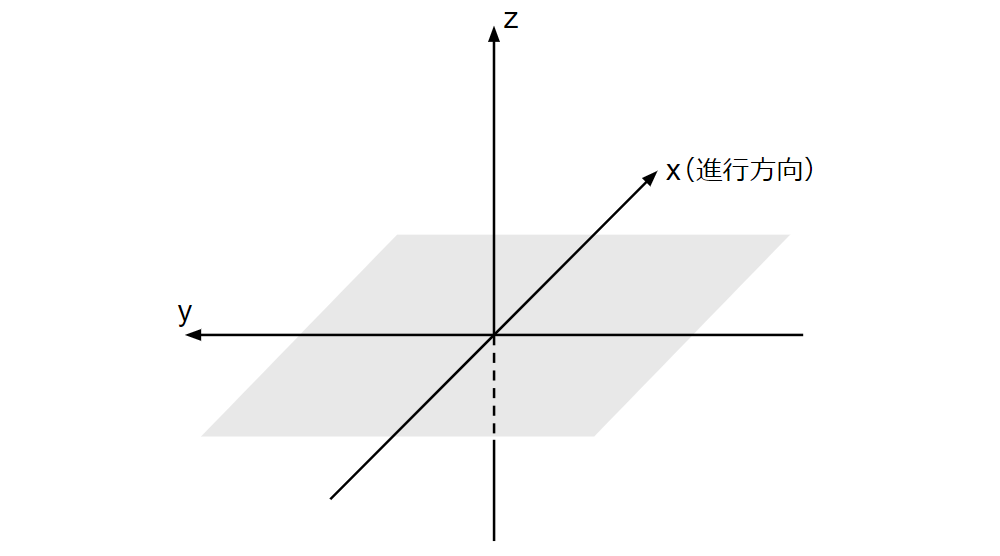
\(x\)軸、\(y\)軸、\(z\)軸それぞれの単位ベクトルを\(\boldsymbol{i}\)、\(\boldsymbol{j}\)、\(\boldsymbol{k}\)とする。

滑走時垂直抗力\(N\)の定義
走っているときの地面、姿勢、風、他者から加わる力、地面から見た速度、原点の真下の地面の点(原点の移動に合わせて移動する)から見た原点の理想の1完歩での平均加速度、といった条件はそのままに、摩擦力が0として接地し滑ったときの仮想の垂直抗力を滑走時垂直抗力\(\boldsymbol{N}\mathrm{\,[N]}\)とする。
\(\boldsymbol{N}=N\boldsymbol{k}\mathrm{\,[N]}\)
\(\boldsymbol{N}\)(\(N\))には、重力や風、他者との接触による\(z\)軸方向の力、地面の\(x\)軸方向の曲率がある場合に生じる\(z\)軸方向の慣性力(遠心力)、低い体勢から高い体勢になるときや高い体勢から低い体勢になるときなどに生じる\(z\)軸方向の慣性力が影響する。

特殊な平均の力の図
特殊な平均の力を考えると、理想の1完歩での加速度やスタンス期の割合を上手く説明できる。
特殊な平均の力は、地面と平行な\(x\)軸と\(y\)軸方向は、理想の1完歩の時間(理想の1完歩での肢が1周する時間)\(T_{u}\mathrm{\,[s]}\)で平均した力、地面に垂直な\(z\)軸方向は、理想の1完歩での全肢のスタンス期の時間の平均\(\bar{T_{uon}}\mathrm{\,[s]}\)で平均した力となる。
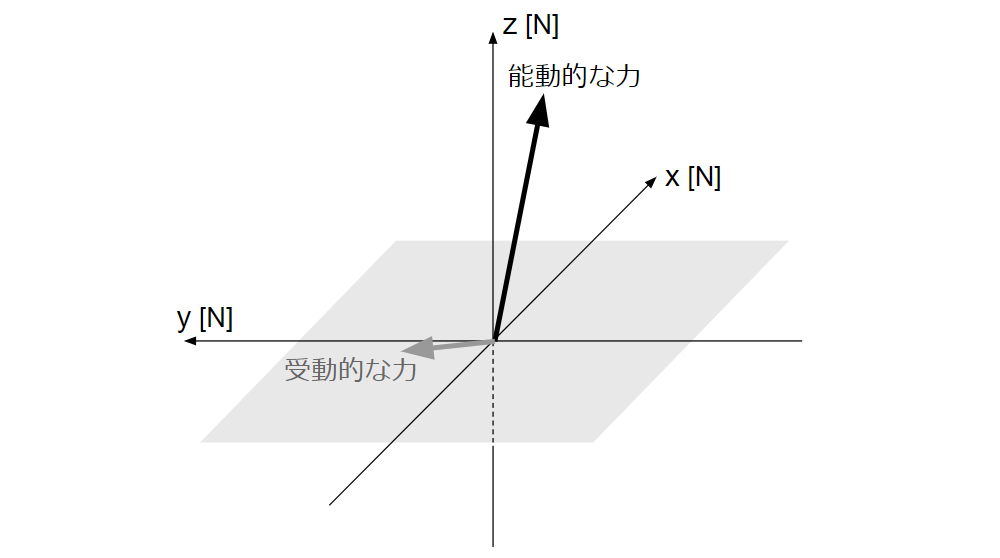
特殊な平均の力には、能動的な力と受動的な力の2つがある。
能動的な力は体の動きと地面(地面と足裏の接地部分の作用)で決まる。
受動的な力は、地面から受ける抗力、風による\(x\)軸と\(y\)軸方向の力(空気抵抗を含む)、地面が水平でない場合の重力による\(x\)軸と\(y\)軸方向の力などが含まれる。

能動的な力
能動的な力を\(\boldsymbol{F}_p\mathrm{\,[N]}\)とすると、
\(\boldsymbol{F}_p=F_{px}\boldsymbol{i}+F_{py}\boldsymbol{j}+F_{pz}\boldsymbol{k}\mathrm{\,[N]}\)
と表せる。
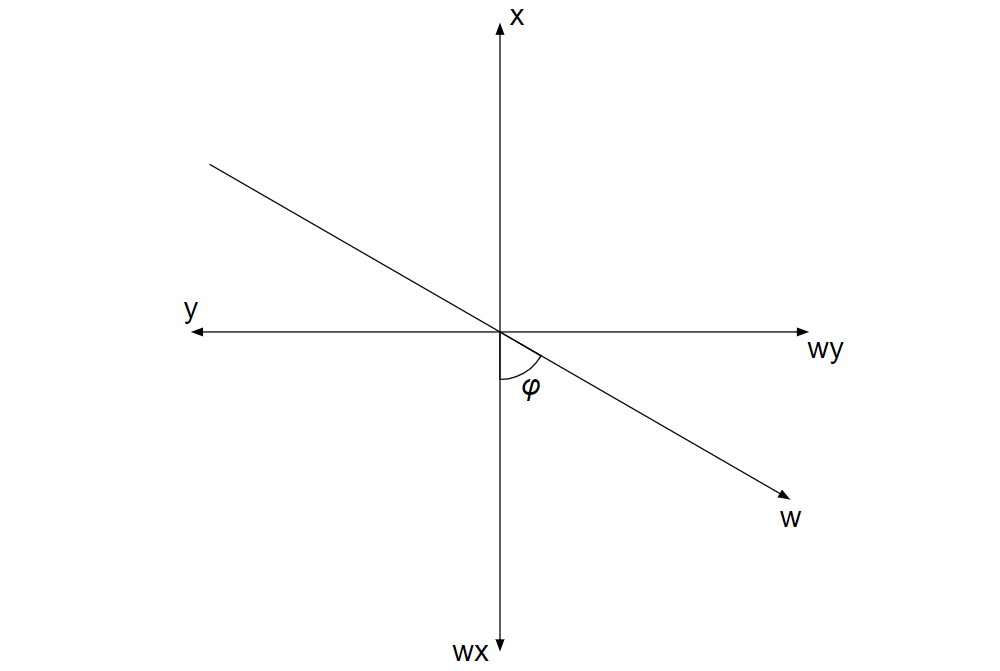
・\(w\)軸、\(wx\)軸、\(wy\)軸の設定
地面と平行な\(F_{px}\boldsymbol{i}+F_{py}\boldsymbol{j}\)の向きに\(w\)軸をとる。
\(w\)軸が\(x\)軸の正の向きとのなす角を\(θ\)とする。
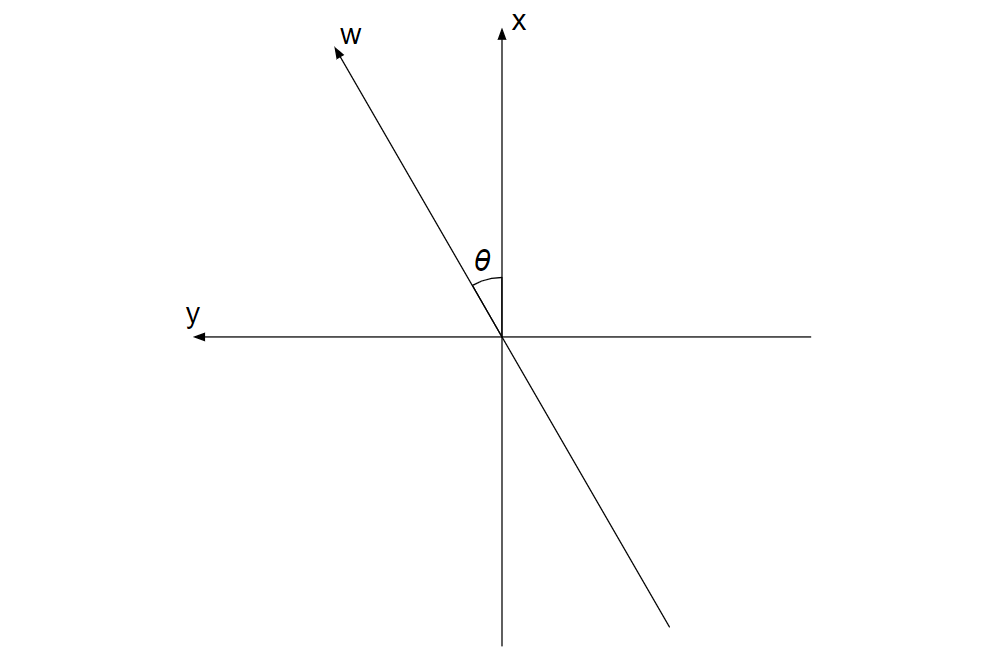
\(w\)軸の単位ベクトルを\(\boldsymbol{l}\)とする。
\(w\)軸を使うと、
\(\boldsymbol{F}_p=F_{pw}\boldsymbol{l}+F_{pz}\boldsymbol{k}\mathrm{\,[N]}\)
と表せる。
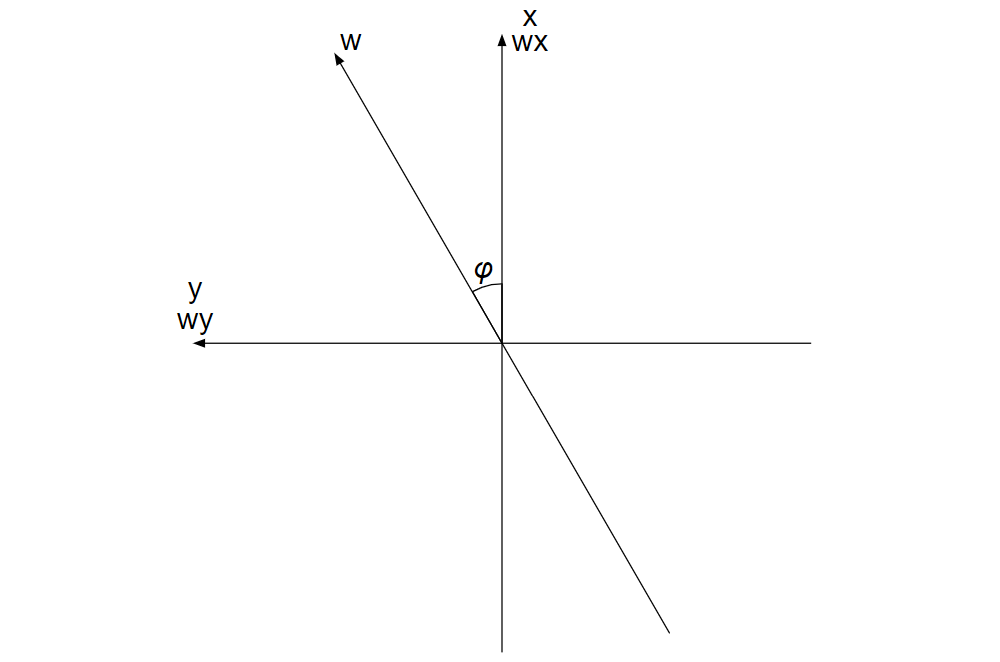
また、\(F_{px}\boldsymbol{i}\)の向きに\(wx\)軸をとり、\(F_{py}\boldsymbol{j}\)の向きに\(wy\)軸をとる。
\(wx\)軸が\(w\)軸とのなす角を\(φ\,(0 \leq φ \leq \displaystyle \frac{π}{2})\)とする。
この軸は今回は特に使用しないが、向心力について考えたり、今回のモデルを拡張して考えたりするときに便利になると思われる。
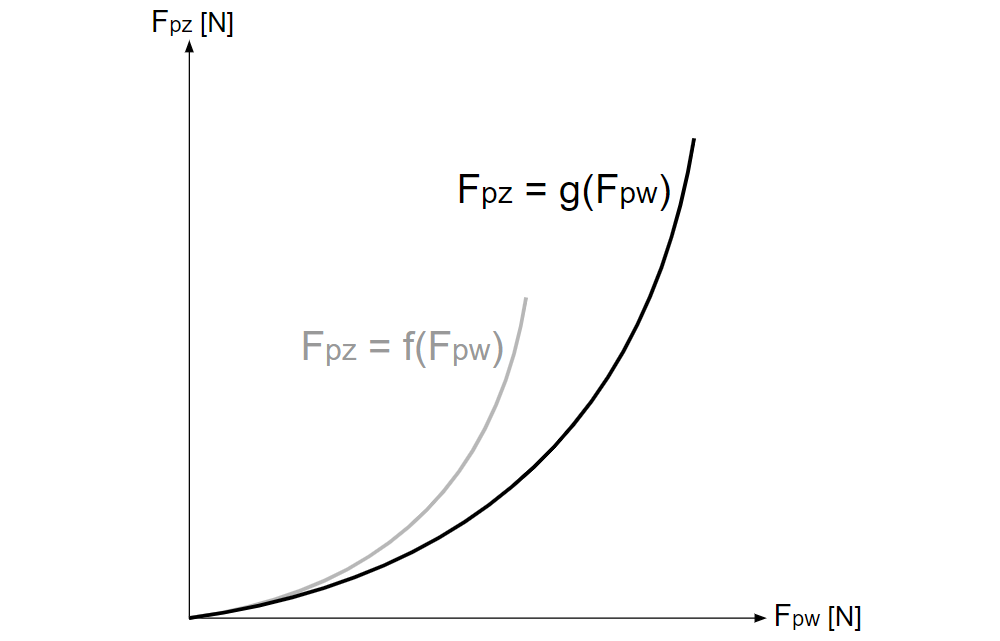
・\(\boldsymbol{F}_p\)の法則
\(F_{pz}\)は\(F_{pw}\)の関数であり、
\(F_{pz}=g(F_{pw})=NAf(\displaystyle \frac{F_{pw}}{NA})\)
とおける。
\(F_{pz}=g(F_{pw})\)のグラフは、\(F_{pz}=f(F_{pw})\)のグラフを原点を中心に\(w\)軸方向、\(z\)軸方向ともに\(NA\)倍したものである。
走能力数:\(A\mathrm{\,[\,]}\)
\(A \gt 0\)
走能力数\(A\)が大きいほど\(N\)に対して大きな\(F_{pw}\)を発揮することができる。基本的には\(A\)が大きいほど速く走ることができる。
\(A\)は元々の骨格や筋力に加え、走る環境やレース中の疲労など、様々な要因で変化する。
\(F_{pw}\)、\(F_{pz}\)は\(0\)以上の値になる。
\(F_{pz}=g(F_{pw})\)において、
\(0 \leq F_{pw} \leq F_{pw\text{-}max}\) , \((F_{pw\text{-}max} \gt 0)\)
\(0 \leq F_{pz} \leq F_{pz\text{-}max}\) , \((F_{pz\text{-}max} \gt 0)\)
である。
また、\(F_{pw}=0\)のとき、\(F_{pz}=0\)となる。
\(f(0)=0\)(\(g(0)=0\))
\(f(F_{pw})\)、\(g(F_{pw})\)はすべての\(F_{pw}\)について連続である。
次を満たす\(F_{pw}\)の値は必ず1つだけ存在する。
\(\begin{eqnarray} \left\{ \begin{array}{l} F_{pz}=bF_{pw}\text{ }(\displaystyle \lim_{h \to +0} \displaystyle \frac{f(0+h)-f(0)}{h} \lt b \leq B) \\ F_{pz}=g(F_{pw}) \\ F_{pw} \neq 0 \end{array} \right. \end{eqnarray}\)
出力数:\(b\mathrm{\,[\,]}\)
最大出力数:\(B\mathrm{\,[\,]}\)
出力数\(b\)が大きいほど、\(F_{pw}\)は大きくなる。
また、
\(\begin{eqnarray} \left\{ \begin{array}{l} z=bw \\ z=f(w) \\ w \neq 0 \end{array} \right. \end{eqnarray}\)
を満たす、\(b\)によって一意に定まる\(w\)の値を\(h(b)\)とすると、
\(F_{pw}=NAh(b)\)
\(F_{pw\text{-}max}=NAh(B)\)
\(F_{pz}=g(NAh(b))=NAf(h(b))\)
\(F_{pz\text{-}max}=g(NAh(B))=NAf(h(B))\)
となる。
実際の\(f(w)\)がどのような関数かはわかっていないが、上記の法則を満たす\(f(w)\)の例として、下に凸で頂点が原点を通る2次関数が挙げられる。
・\(\boldsymbol{F}_p\)の性質
\(\boldsymbol{F}_p\)の特に重要な性質を説明する。
・ある出力数\(b\)での\(\displaystyle \frac{F_{pw}}{N}\)、\(\displaystyle \frac{F_{pz}}{N}\)の大きさは、走能力数\(A\)に比例する。
(ある出力数\(b\)での\(F_{pw}\)、\(F_{pz}\)の大きさは、\(NA\)に比例する。)
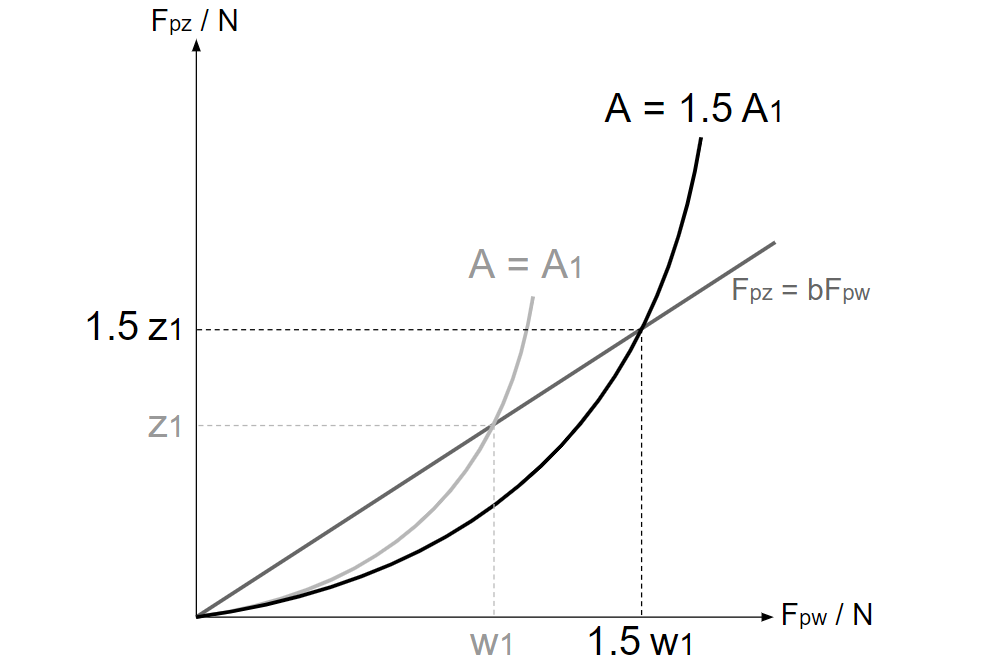
・\(\displaystyle \frac{F_{pw}}{N}\)が同じであれば、走能力数\(A\)が大きいほど出力数\(b\)が小さくなり、\(\displaystyle \frac{F_{pz}}{N}\)が小さくなる。
(\(F_{pw}\)が同じであれば、\(NA\)が大きいほど出力数\(b\)が小さくなり、\(F_{pz}\)が小さくなる。)
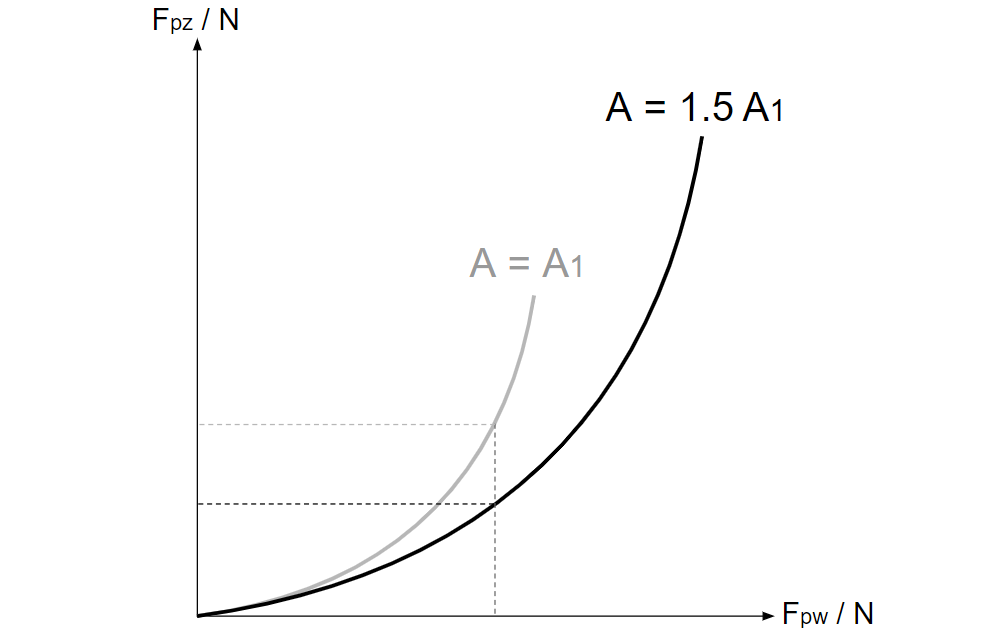
この性質は、全力を出して走るときと力を抜いて走るときとでは、単に発揮する筋力が異なるだけでなく、肢の動かし方も異なることが原因と予想している。

走能力数\(A\)の変化
走能力数\(A\)は元々の骨格や筋力に加え、走る環境やレース中の疲労など、様々な要因で変化する。
環境で変化する一例として、陸上100メートル競走で、加速局面と減速局面で\(A\)が変化する事象が挙げられる。一般的に前半型と言われる選手は、加速局面で\(A\)が大きくなり、減速局面で\(A\)が小さくなる。反対に後半型と言われる選手は、加速局面で\(A\)は小さくなり、減速局面で\(A\)が大きくなる。
\(A\)の変化は、他にも地面の変化や、勾配の変化などで起こる。
そして疲労による\(A\)の減少は、疲労しにくくなる効果のあるドーピングの有無が大きくかかわってくる。レース中は100mという短い距離でも全力を出せば\(A\)は減少する。この疲労による\(A\)の減少が、ドーピングをしている個体とそうでない個体とでは大きく異なる。

受動的な力
受動的な力を\(\boldsymbol{F}_r\mathrm{\,[N]}\)とすると、
\(\boldsymbol{F}_r=\displaystyle\sum_{i=1}\boldsymbol{F}_{ri}\mathrm{\,[N]}\)
と表せる。
受動的な力は、地面から受ける基本の力(\(i=1,2\))とそれ以外の受動的な力(\(i \geq 3\))に分けられる。
・地面から受ける基本の力(\(i=1,2\)):\(\boldsymbol{F}_{r1}+\boldsymbol{F}_{r2}\mathrm{\,[N]}\)
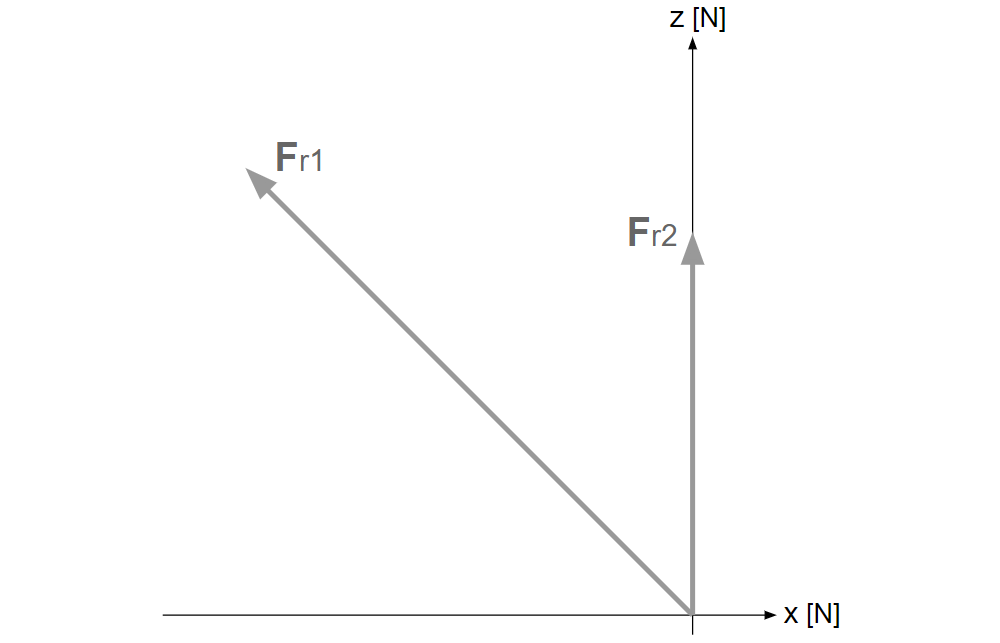
\(\boldsymbol{F}_{r2}\)は\(z\)軸方向で大きさが\(N\)の平均の力である。
\(\boldsymbol{F}_{r2}=N\boldsymbol{k}\mathrm{\,[N]}\)
\(\boldsymbol{F}_{r1}\)は\(x\)軸方向と\(z\)軸方向の平均の力で構成される。
\(\boldsymbol{F}_{r1}=F_{r1x}\boldsymbol{i}+F_{r1z}\boldsymbol{k}\mathrm{\,[N]}\)
\(\boldsymbol{F}_{r1}\)は、地面から見た理想の1完歩での平均の速さ\(v_{ux}\)、\(N\)、地面(地面と足裏の接地部分の作用)で決まる。
\(F_{r1x}\)は\(0\)以下、\(F_{r1z}\)は\(0\)以上の値を取る。
\(F_{r1x} \leq 0\)
\(F_{r1z} \geq 0\)
\(-F_{r1x}\)と\(F_{r1z}\)は、地面から見た理想の1完歩での平均の速さ\(v_{ux}\)におおよそ比例して大きくなると予想している。
\(v_{ux}=0\)のときは、\(-F_{r1x}=0\)、\(F_{r1z}=0\)になる。
\(-F_{r1x}\)、\(F_{r1z}\)は\(N\)におおよそ比例して大きくなると予想している。
\(N=0\)のときは、\(-F_{r1x}=0\)、\(F_{r1z}=0\)になる。
・それ以外の受動的な力(\(i \geq 3\)):\(\displaystyle\sum_{i=3}\boldsymbol{F}_{ri}\mathrm{\,[N]}\)
ここには風による\(x\)軸と\(y\)軸方向の力(空気抵抗を含む)、地面が水平でない場合の重力による\(x\)軸と\(y\)軸方向の力などが含まれる。特殊なところでは、芝を踏んだときに芝が伸びている向きに地面から肢に加わる力、レース中に他の人や馬に接触したときに加わる力などがある。
\(z\)軸方向の力は0になる。これは\(z\)軸方向の力は既に\(N\)に含まれているためである。

特殊な平均の力と地面から見た理想の1完歩での平均加速度
地面から見た理想の1完歩での平均加速度は下のようになる。
地面から見た理想の1完歩での平均加速度:\(\boldsymbol{a}_u=a_{ux}\boldsymbol{i}+a_{uy}\boldsymbol{j}+a_{uz}\boldsymbol{k}\mathrm{\,[m\,s^{-2}]}\)
進行方向(\(x\)軸方向)の理想の1完歩での平均加速度:\(a_{ux}=\displaystyle \frac{F_{px}+F_{rx}}{m}\)
向心力方向(\(y\)軸方向)の理想の1完歩での平均加速度:\(a_{uy}=\displaystyle \frac{F_{py}+F_{ry}}{m}\)
(縦方向、縦の向心力方向(\(z\)軸方向)の理想の1完歩での平均加速度:\(a_{uz}\))
また、\(\boldsymbol{F}_p\)と\(\boldsymbol{F}_{r1}\)を使い、地面から見た理想の1完歩での能動的な平均加速度を下のように定義する。
地面から見た理想の1完歩での能動的な平均加速度:\(\boldsymbol{a}_{u1}=a_{u1x}\boldsymbol{i}+a_{u1y}\boldsymbol{j}\mathrm{\,[m\,s^{-2}]}\)
進行方向(\(x\)軸方向)の理想の1完歩での能動的な平均加速度:\(a_{u1x}=\displaystyle \frac{F_{px}+F_{r1x}}{m}\)
向心力方向(\(y\)軸方向)の理想の1完歩での能動的な平均加速度:\(a_{u1y}=\displaystyle \frac{F_{py}}{m}\)
地面から見た能動的な加速度とは、地面から受ける基本の力以外の受動的な力\(\displaystyle\sum_{i=3}\boldsymbol{F}_{ri}\)を無視したときの、地面から見た\(x\)軸と\(y\)軸方向と仮想の加速度である。

特殊な平均の力とスタンス期の割合
理想の1完歩での肢が1周する時間(1完歩の時間):\(T_u\mathrm{\,[s]}\)
理想の1完歩での全肢のスタンス期の時間の平均:\(\bar{T_{uon}}\mathrm{\,[s]}\)
とする。
このとき、
\(NT_u=(F_{pz}+F_{r1z}+N)\bar{T_{uon}}\)
が成り立つ。
スタンス期の割合\(\displaystyle \frac{\bar{T_{uon}}}{T_u}\)は、
\(\displaystyle \frac{\bar{T_{uon}}}{T_u}=\displaystyle \frac{N}{F_{pz}+F_{r1z}+N}\)
ここから次のことが導かれ、それは私の目視での観察結果と矛盾しない。
・加速度0、一定の速度で走る場合、空気抵抗の影響を無視できる大きさだと考えると、走能力数\(A\)が大きいほど\(F_{pz}\)が小さくなり、スタンス期の割合が大きくなる。
→レース中に安定した速度で走る場合は、走能力数\(A\)が大きいほどスタンス期の割合が大きくなる。
・ある速度のときに一定の出力数\(b\)で走る場合、走能力数\(A\)が大きいほど\(F_{pz}\)が大きくなり、スタンス期の割合が小さくなる。
→スタート時に最大出力数で走る場合は、走能力数\(A\)が大きいほどスタンス期の割合が小さくなる。
・ある人(馬)が加速度0、一定の出力数\(b\)で走るとき、走能力数\(A\)の変化が無視できる大きさだと考えると、水平な地面を走る場合と比べて、上り坂だと\(v_{ux}\)と\(F_{r1z}\)が小さくなり、スタンス期の割合が大きくなる。下り坂だと\(v_{ux}\)と\(F_{r1z}\)が大きくなり、スタンス期の割合が小さくなる。
→基本的には上り坂を走るとスタンス期の割合が大きくなり、下り坂を走るとスタンス期の割合が小さくなる。
・ある人(馬)が水平な地面を一定の速度で走る場合、コーナーの半径が小さく理想の1完歩での平均の向心力\(F_{pwy}\)が大きいほど\(F_{pz}\)が大きくなり、スタンス期の割合が小さくなる。
→一定の速度を保って走る場合、基本的にはコーナーを曲がるときは直線を走るときと比べスタンス期の割合が小さくなる。
・ある人(馬)が水平な地面を一定の出力数で走る場合、コーナーの半径が小さく\(v_{ux}\)が小さいほど\(F_{r1z}\)が小さくなり、スタンス期の割合が大きくなる。
→一定の出力数で走る場合(全力で走る場合など)、基本的にはコーナーを曲がるときは直線を走るときと比べスタンス期の割合が大きくなる。
また、基本的に速く走るほどスタンス期の割合が小さくなる(接地時間が短くなる)が、これは必然的にそうなるのであり、一般的に言われている「スタンス期の割合を小さくする(接地時間を短くする)ことを”意識すれば”速く走れる」との論説は間違いであることがわかる。

早期負重度\(s\)
ある一つの肢\(i\)の地面から肢に加わる力\(\boldsymbol{F}_i(t)\mathrm{\,[N]}\)、着地したときの時間\(t_{oni}\mathrm{\,[s]}\)、スタンス期の時間\(T_{oni}\mathrm{\,[s]}\)を使って、ある肢の早期負重度\(s_i\)を次のように定義する。
\(s_i=\displaystyle \frac{\displaystyle \int_{t_{oni}}^{t_{oni}+T_{oni}} |\boldsymbol{F}_i(t)|\displaystyle \frac{T_{oni}-(t-t_{oni})}{T_{oni}} dt}{\displaystyle \int_{t_{oni}}^{t_{oni}+T_{oni}} |\boldsymbol{F}_i(t)| dt}\)
\(0 \leq s_i \leq 1\)
偽速度\(d=0\)のときの理想の1完歩でのある肢の早期負重度を\(s_{u0i}\)とする。偽速度については後ほど説明する。
これが基本の早期負重度になり、早期負重度の変化量を\(\Delta s_i=s_i-s_{u0i}\)とする。(理想の1完歩での早期負重度の変化量を\(\Delta s_{ui}=s_{ui}-s_{u0i}\)とする。)
ただし、早期負重度は地面(地面と足裏の接地部分の作用)によっても変化するので、早期負重度の変化量を扱う場合は基本的に地面が変わらない状況を想定する。

正の値をとる力の力積
地面からある一つの肢\(i\)に加わる\(w\)軸方向の力を\(F_{wi}(t)\mathrm{\,[N]}\)とする。
また、\(F_{wi\text{-}plus}(t)\mathrm{\,[N]}\)を次のように定義する。
\(F_{wi}(t) \geq 0\)のとき、\(F_{wi\text{-}plus}(t)=F_{wi}(t)\)
\(F_{wi}(t) \lt 0\)のとき、\(F_{wi\text{-}plus}(t)=0\)
1完歩の時間\(T\mathrm{\,[s]}\)を使い、\(I_{w\text{-}plusT}\mathrm{\,[Ns]}\)を次のように定義する。
\(I_{w\text{-}plusT}=\displaystyle \sum_{i=1}^{n} \displaystyle \int_{t_1}^{t_1+T} F_{wi\text{-}plus}(t) dt\)
これを\(NT\)で割ると、\(\displaystyle \frac{I_{w\text{-}plusT}}{NT}\)になる。
理想の1完歩でのこれらを、
\(I_{uw\text{-}plusTu}\)、\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)
とする。

\(F_{pw}\text{-}A\)グラフ
縦軸に\(F_{pw}\mathrm{\,[N]}\)、横軸に\(A\mathrm{\,[\,]}\)をとった\(F_{pw}\text{-}A\)グラフを考える。
そこに、\(F_{pw}=F_{pw\text{-}max}=NAh(B)\)の直線を引く。
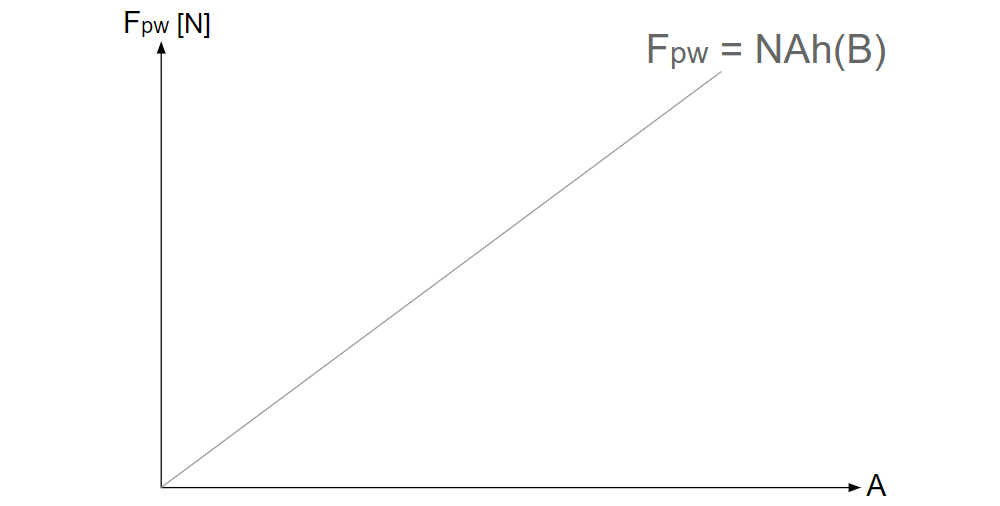
このグラフは、偽速度\(d\)を幾何学的に理解するのに便利なグラフである。

偽速度\(d\)の導入
目視ではあるが、観察した結果から、おおよそ次のことがわかっている。
・走能力数\(A\)が異なる場合、同じ環境を同じ速度で走ったとき(\(N\), \(\boldsymbol{F}_r\), \(F_{pw}\), \(F_{px}\)が一定)、\(A\)が大きいほど、\(\Delta s_{ui}\,(i=1,…,n)\)が小さくなり、\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)が大きくなる。
・走能力数\(A\)が異なる場合でも、\(F_{pw}=F_{px}=-F_{r1x}=NAh(B)\)のときは、\(\Delta s_{ui}\,(i=1,…,n)\)と\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)は一定である。
これは地面と肢の速度、および地面への力の加えやすさの違いが原因と考えられ、偽速度\(d\mathrm{\,[\,]}\)を導入すると説明と計算が容易になる。
\(d\)は大きいほど、\(\Delta s_{ui}\,(i=1,…,n)\)が小さくなり、\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)が大きくなる。
\(\displaystyle \frac{\partial}{\partial d}\Delta s_{ui} \lt 0\) \((\displaystyle \frac{\partial}{\partial d} s_{ui} \lt 0)\)
\(\displaystyle \frac{\partial}{\partial d}\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u} \gt 0\)
偽速度\(d\)を考えるときは、\(F_{pw} \gt 0\)のときに限る。
・\(θ=0\), \(F_{pw}=F_{px}=-F_{r1x}\)のときの\(d\)
地面から見た理想の1完歩での能動的な平均加速度がない最も基本的な状態である。このとき\(d\)に関して、
\(dN=NAh(B)-F_{pw}\)
が成り立つ。
\(F_{pw}=F_{px}=-F_{r1x}=NAh(B)\)のとき、\(d=0\)になる。
\(F_{pw}=NAh(B)-dN\)と変形できるので、\(F_{pw}\text{-}A\)グラフにおいて、\(d\)の等値線は\(F_{pw}=NAh(B)\)の直線と平行になる。
ここから次のことが導かれ、それは私の目視での観察結果と矛盾しない。
・\(\displaystyle \frac{F_{pw}}{N}\)が同じであれば、\(A\)が大きいほど\(d\)が大きくなる。
・\(A,\,N\)が同じであれば(同じ人や馬が同じ条件で走る場合など)、\(F_{pw}\)が小さいほど\(d\)が大きくなる。
・\(θ=0\), \(F_{pw}=F_{px} \neq -F_{r1x}\)のときの\(d\)
進行方向と\(F_{pw}\)の向きが同じで、地面から見た理想の1完歩での向心力方向の能動的な平均加速度はないが、進行方向の能動的な平均加速度がある状態である。このとき\(d\)に関して次のことが成り立つ。
\(d_1N=NAh(B)-(-F_{r1x})\)
\(d_2N=NAh(B)-F_{pw}\)
とすると、
\(dN=d_2N+C(NAh(B)-d_2N)-C(NAh(B)-d_1N)\)
\(d=d_2+C(Ah(B)-d_2)-C(Ah(B)-d_1)\) …①
\(dN=d_2N+C(d_1N-d_2N)\)
\(d=d_2+C(d_1-d_2)\)
\(dN=NAh(B)-F_{pw}+C(F_{pw}+F_{r1x})\)
加速度補正数:\(C\mathrm{\,[\,]}\)
\(C>1\)
これは\(F_{pw}=F_{px}=-F_{r1x}\)のときも成り立つ。
またこれは、次の原則から導いたものである。
・\(d_1=d_2\)のとき(地面から見た理想の1完歩での進行方向の能動的な平均加速度が0のとき)、\(d=d_1=d_2\)となる。
・\(d_1 \gt d_2\)のとき(地面から見た理想の1完歩での進行方向の能動的な平均加速度が正のとき)、\(d \gt d_1 \gt d_2\)となる。
・\(d_1 \lt d_2\)のとき(地面から見た理想の1完歩での進行方向の能動的な平均加速度が負のとき)、\(d \lt d_1 \lt d_2\)となる。
・偽速度の原理から考えて、\(d=\)[肢の絶対偽速度]\(–\)[地面の偽速度]の構造をする。
・地面の偽速度は、\(-\displaystyle \frac{F_{r1x}}{N}\)に比例する。(進行方向と\(F_{pw}\)の向きが同じ場合。)
式①において、\(d_2+C(Ah(B)-d_2)\)の部分が(肢の)絶対偽速度、\(C(Ah(B)-d_1)\)の部分が地面の偽速度である。
絶対偽速度は\(Ah(B)+(C-1)\displaystyle \frac{F_{pw}}{N}\)、地面の偽速度は\(-C \displaystyle \frac{F_{r1x}}{N}\)となる。(進行方向と\(F_{pw}\)の向きが同じ場合。)
\(d_2=0\)のときの絶対偽速度は\(CAh(B)\)。
また、\(d_2 \to Ah(B)-0\)のときの絶対偽速度は\(\displaystyle \lim_{d_2 \to Ah(B)-0}(d_2+C(Ah(B)-d_2))=Ah(B)\)。
つまり、加速度補正数\(C\)とは、\(d_2 \to Ah(B)-0\)のときの絶対偽速度に対する\(d_2=0\)のときの絶対偽速度の比である。
・\(θ \neq 0\)のときの\(d\)
進行方向と\(F_{pw}\)の向きが異なる状態。このとき偽速度\(d\)に関して次のことが成り立つ。
\(d_1N=NAh(B)-(-F_{r1x}\cos θ)\)
\(d_2N=NAh(B)-F_{pw}\)
とすると、
\(dN=d_2N+C(d_1N-d_2N)\)
\(d=d_2+C(d_1-d_2)\)
\(dN=NAh(B)-F_{pw}+C(F_{pw}+F_{r1x}\cos θ)\)
\(F_{r1w}=F_{r1x}\cos θ\)であるから、次のようにも書ける。
\(d_1N=NAh(B)-(-F_{r1w})\)
\(d_2N=NAh(B)-F_{pw}\)
とすると、
\(dN=d_2N+C(d_1N-d_2N)\)
\(d=d_2+C(d_1-d_2)\)
\(dN=NAh(B)-F_{pw}+C(F_{pw}+F_{r1w})\)
これは\(θ=0\)のときも成り立つ。

偽速度\(d\)の幾何学的理解
・偽速度と絶対偽速度の等値線
\(F_{pw}\text{-}A\)グラフに偽速度\(d\)の等値線を描くと、その傾きは\(Nh(B)\)となり、\(F_{pw}=NAh(B)\)の直線と平行になる。
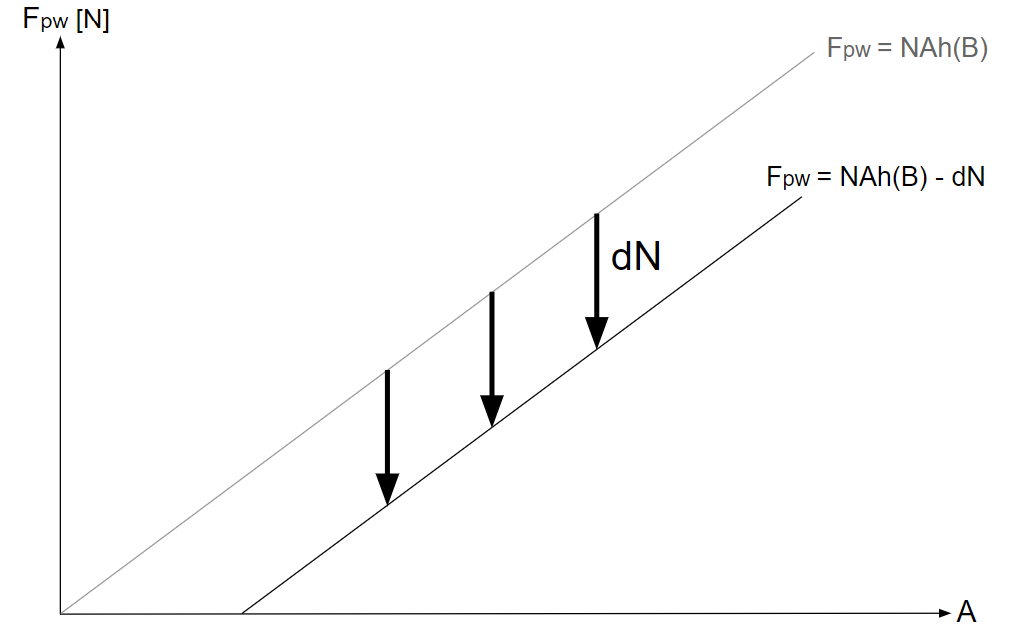
\(F_{pw}\text{-}A\)グラフに絶対偽速度\(d_2+C(Ah(B)-d_2)\)の等値線を引くと、その傾きは\(-\displaystyle \frac{Nh(B)}{C-1}\)となる。
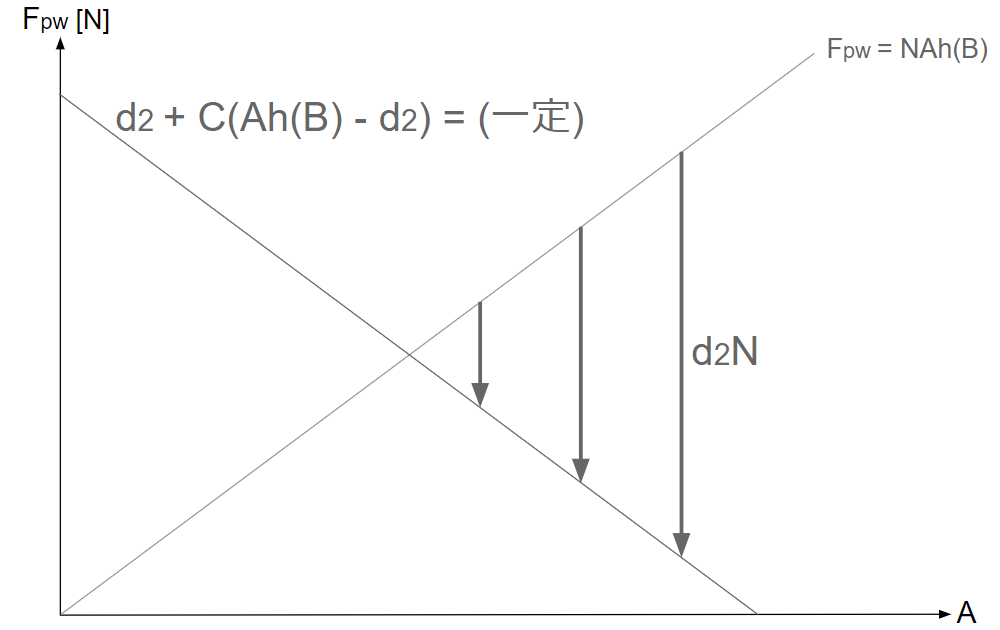
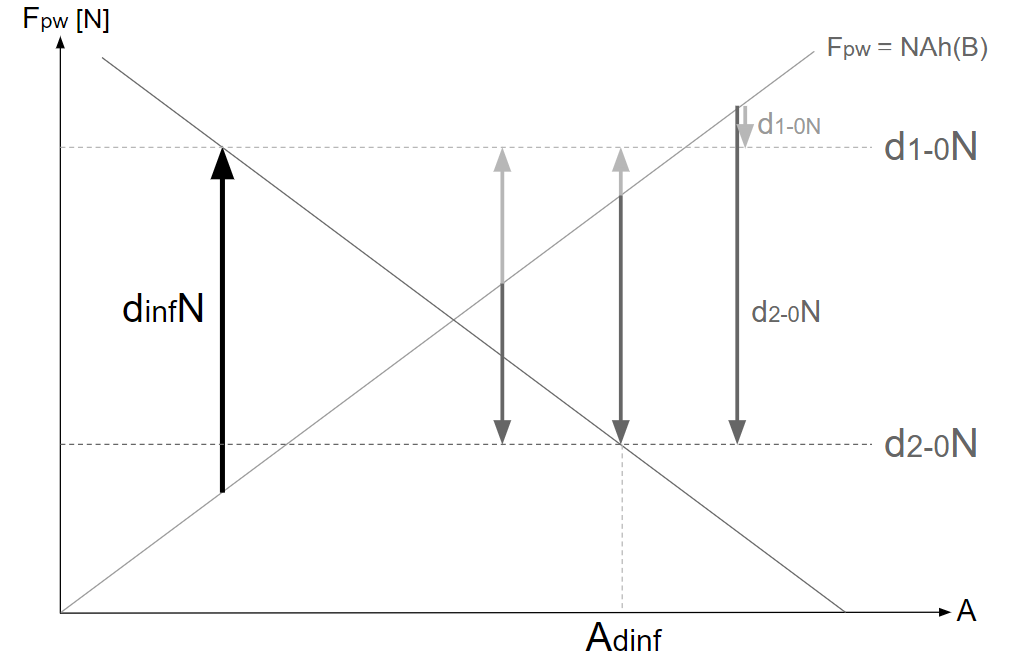
・\(F_{pw}\text{-}A\)グラフに\(d_1\)、\(d_2\)を描く
ある\(A\)での\(d_1N\)、\(d_2N\)は次のように描かれる。
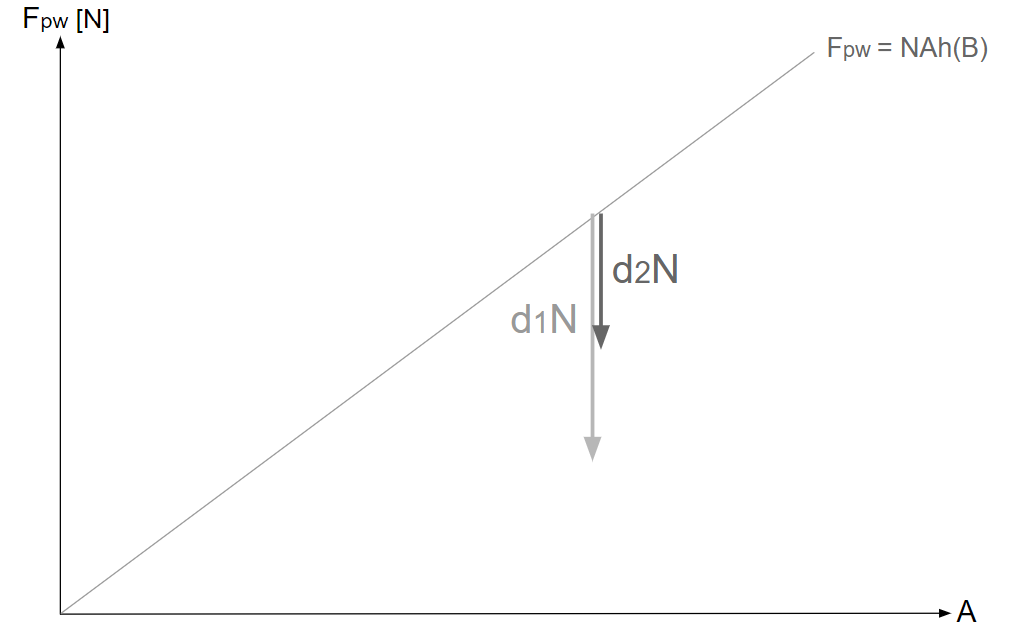
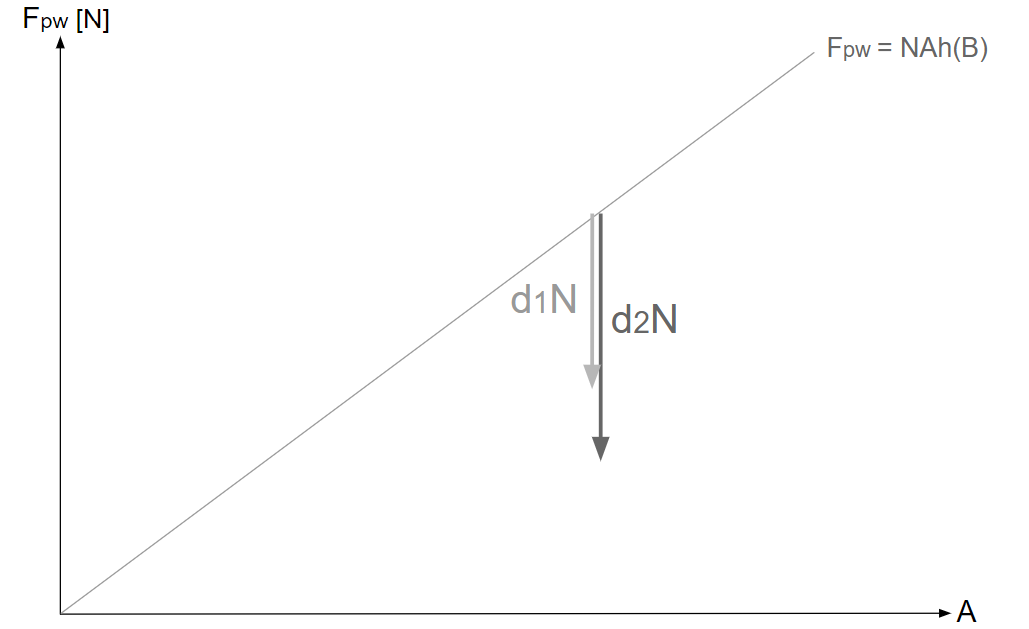
そして、\(d_1N-d_2N\)は次のように描かれる。
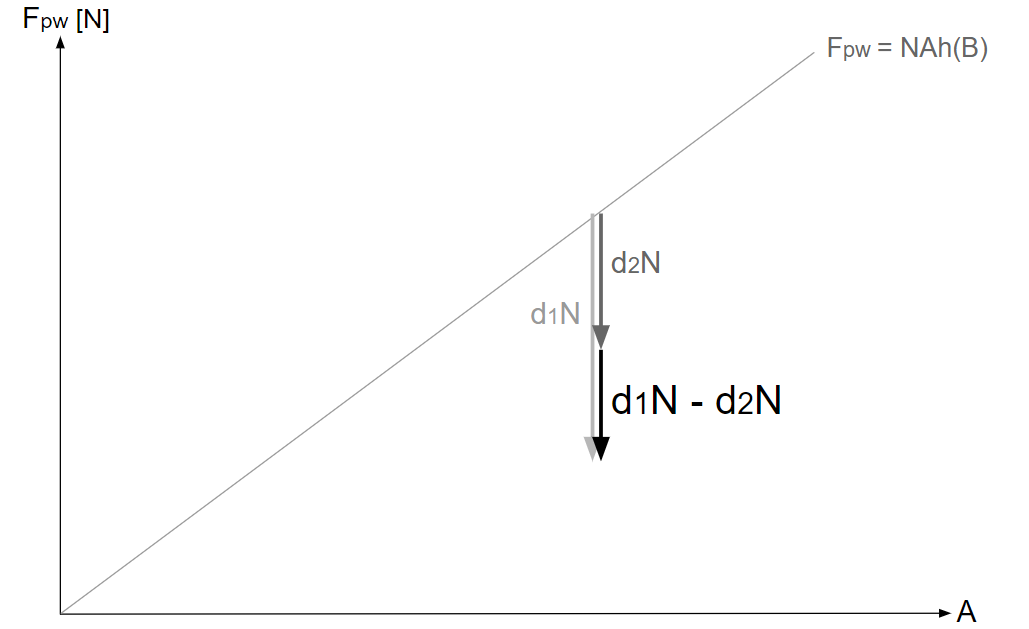
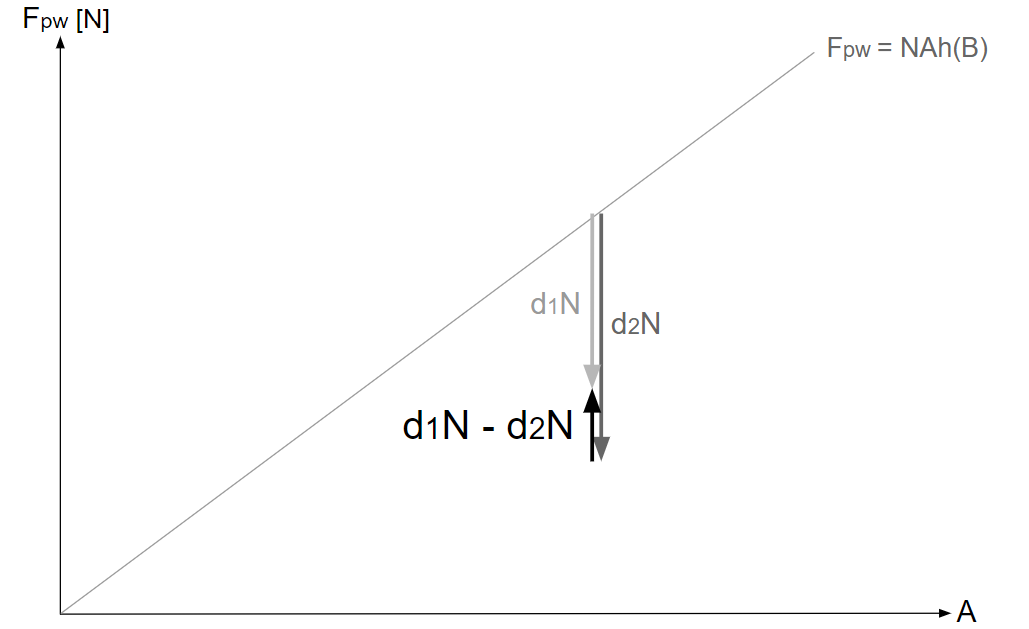
・\(F_{pw}\text{-}A\)グラフ上で\(d_1\)と\(d_2\)から\(d\)を求める
\(dN=d_2N+C(d_1N-d_2N)\)であるから、ある\(A\)での\(dN\)は次のように描かれる。
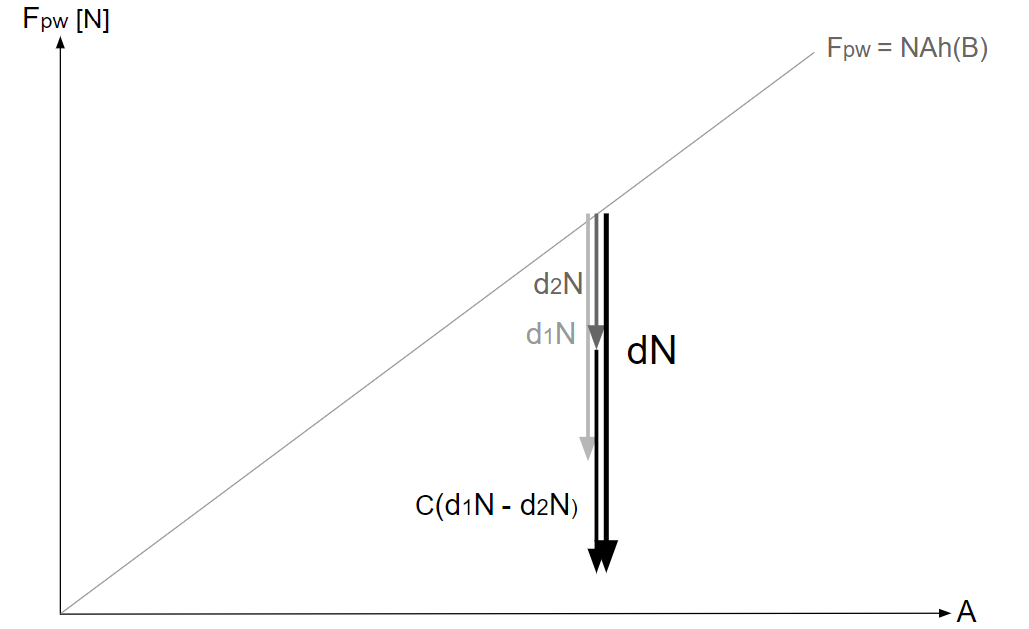
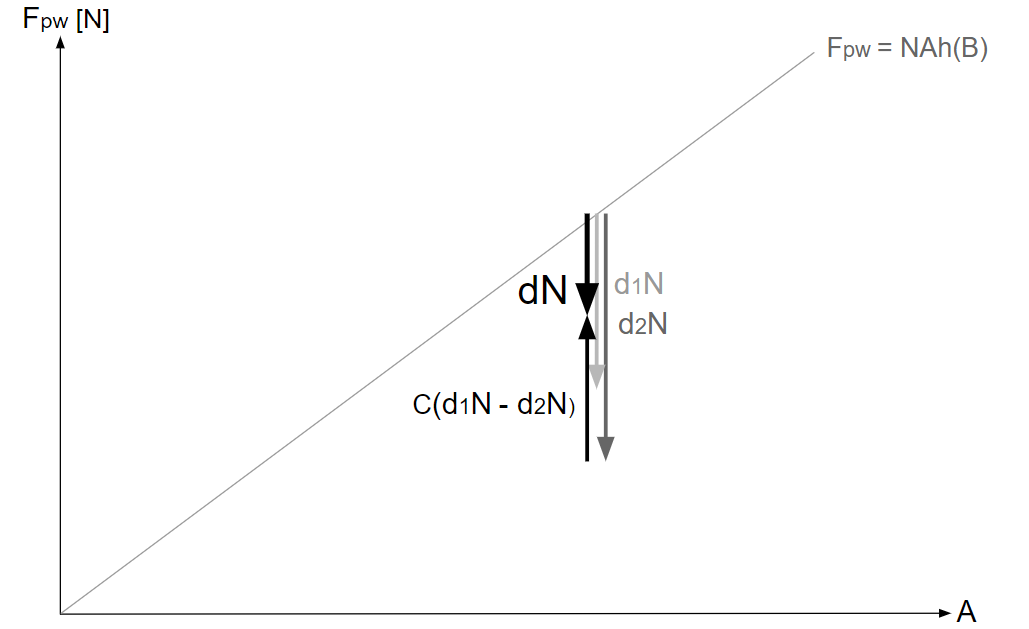
また、\(dN\)は次の方法でも求められる。
ある\(A\)(\(A_1\))での\(d_1N\)の終点を通る、\(A\)軸に平行な直線を引く。
\(A_1\)での\(d_2N\)の終点を通る、絶対偽速度の等値線を引く。
2本の直線の交点の\(A\)を\(A_2\)とすると、\(A_2\)における2直線の交点を終点とする\(dN\)は、\(A_1\)の\(dN\)と等しくなる。
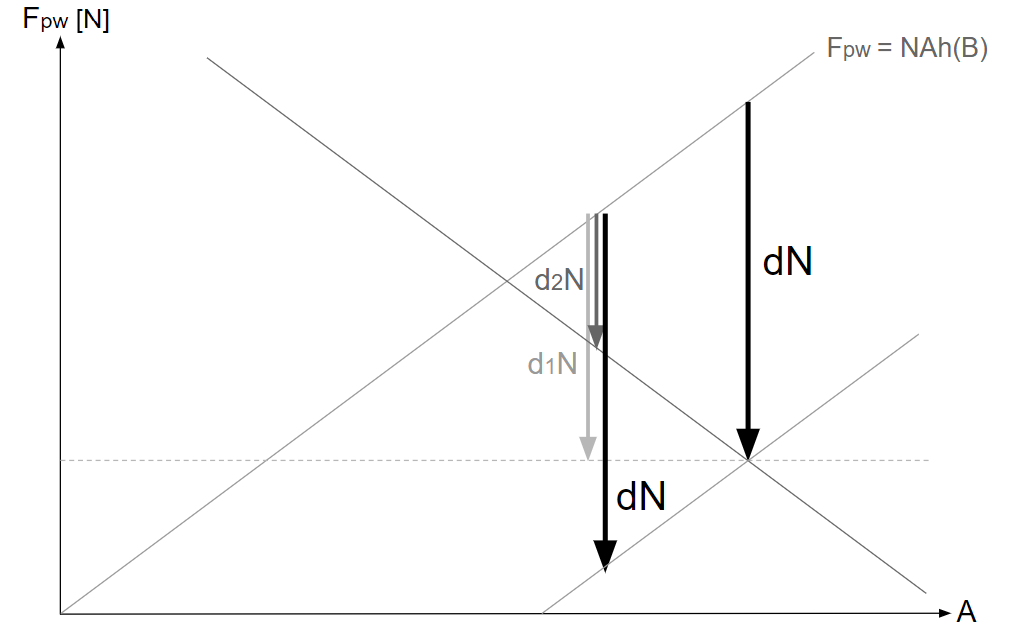
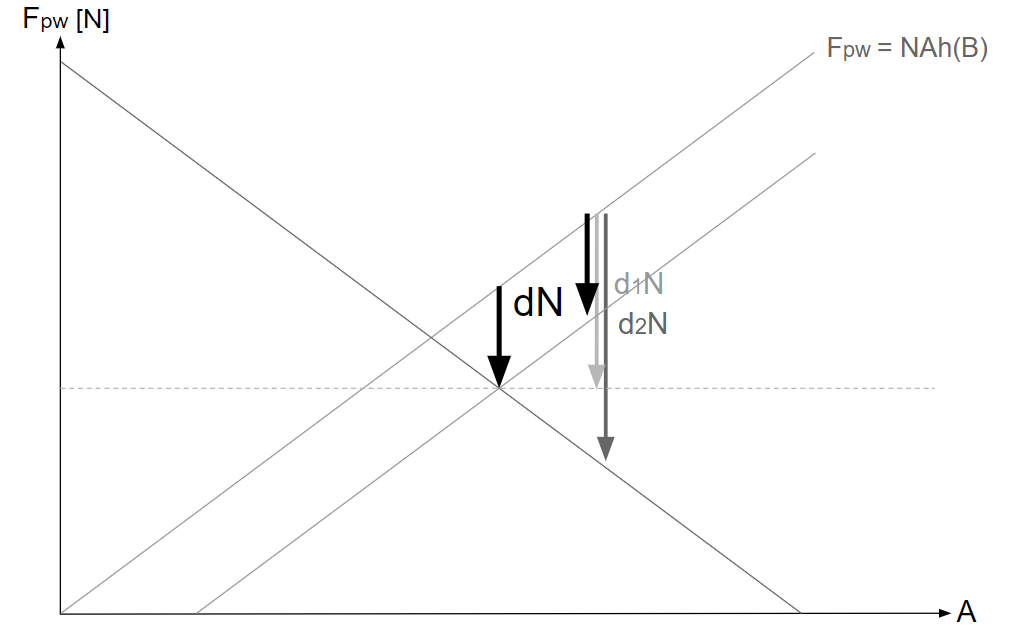

偽速度\(d\)と\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)の関係についての予想
\(d\)は大きいほど、\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)が大きくなる。これについて、次のような関係が予想される。
\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}=E_1d+E_2\)
\(E_1\)、\(E_2\)は無次元の正の定数。
\(d=0\)のとき、\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}=E_2\)になる。
\(0=E_1d+E_2\)のときの\(d\)を\(d_{inf}\)とする。
\(d_{inf}\)以下の\(d\)の場合、走りを維持できなくなり、滑るか転ぶと予想される。
走りを維持できないため、\(d_{inf}\)以下の\(d\)の場合、\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}=E_1d+E_2\)は成り立たなくなる。つまり、この関数の定義域は、\(d_{inf} \lt d\)である。
・下り坂で走りを維持したまま止まれるときとそうでないとき
\(d_{inf}\)以下の\(d\)の場合、走りを維持できなくなるという予想が正しいとすると、下り坂で走りを維持したまま止まれるときとそうでないときの判別ができる。
風や空気抵抗の影響を考えず、一定の角度の下り坂を加速度0、ある速度で走っているという初期条件を与えたとき、まっすぐ走る場合に走りを維持したまま止まれるどうかは走能力数\(A\)によって決まる。
まず、初期条件の速度のときの\(F_{r1x}\)を\(F_{r1x0}\)とすると、初期条件の\(d_1\)は、
\(d_1N=NAh(B)+F_{r1x0}\)
に決定される。この\(d_1\)を\(d_{1\text{-}0}\)とする。
次に、初期条件の速度を維持する\(d_2\)を考える。
重力による\(x\)軸方向の力を\(F_{r3x}\)とすると、初期条件の速度を維持する\(F_{pw}\)は、
\(F_{pw}=-F_{r1x0}-F_{r3x}\)
初期条件の速度を維持する\(d_2\)は、
\(d_2N=NAh(B)+F_{r1x0}+F_{r3x}\)
この\(d_2\)を\(d_{2\text{-}0}\)とする。
\(d_{1\text{-}0}\)、\(d_{2\text{-}0}\)のときの\(d\)を\(d_0\)とすると、
\(d_0N=d_{2\text{-}0}N+C(d_{1\text{-}0}N-d_{2\text{-}0}N)\)
\(d_0N=NAh(B)+F_{r1x0}+F_{r3x}-CF_{r3x}\)
となる。
\(d_0\)は\(A\)の関数であり、\(A\)が大きいほど。\(d_0\)は大きくなる。
\(d_0=d_{inf}\)となる\(A\)を\(A_{dinf}\)とする。
\(A\)が変化しないものとすると、
\(A \gt A_{dinf}\)の場合、\(d_0 \gt d_{inf}\)となり、走りを維持したまま止まることができる。
\(A \leq A_{dinf}\)の場合、\(d_0 \leq d_{inf}\)となり、加速した後に走りを維持できなくなるか、初期条件が与えられた瞬間に走りを維持できなくなる。

\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)と後肢負重率
馬などの四足歩行の動物において、地面から前肢に加わる力を\(\boldsymbol{F}_{front}(t)\mathrm{\,[N]}\)、地面から後肢に加わる力を\(\boldsymbol{F}_{hind}(t)\mathrm{\,[N]}\)とする。1完歩の時間\(T\mathrm{\,[s]}\)を使って、後肢負重率\(H\)を次のように定義する。
\(H=\displaystyle \frac{\displaystyle \int_{t_1}^{t_1+T} |\boldsymbol{F}_{hind}(t)| dt}{\displaystyle \int_{t_1}^{t_1+T} (|\boldsymbol{F}_{front}(t)|+|\boldsymbol{F}_{hind}(t)|) dt}\)
理想の1完歩での後肢負重率を\(H_u\)とする。
地面からある一つの肢\(i\)に加わる\(w\)軸方向の力\(F_{wi}(t)\mathrm{\,[N]}\)を使い、\(F_{wi\text{-}minus}(t)\mathrm{\,[N]}\)を次のように定義する。
\(F_{wi}(t) \gt 0\)のとき、\(F_{wi\text{-}minus}(t)=0\)
\(F_{wi}(t) \leq 0\)のとき、\(F_{wi\text{-}minus}(t)=F_{wi}(t)\)
1完歩の時間\(T\mathrm{\,[s]}\)を使い、\(I_{w\text{-}minusT}\mathrm{\,[Ns]}\)を次のように定義する。
\(I_{w\text{-}minusT}=\displaystyle \sum_{i=1}^{n} \displaystyle \int_{t_1}^{t_1+T} F_{wi\text{-}minus}(t) dt\)
理想の1完歩でのこれを\(I_{uw\text{-}minusTu}\)とする。
\(I_{uw\text{-}plusTu}\)、\(I_{uw\text{-}minusTu}\)、\(F_{pw}\)、\(F_{r1w}\)に関して以下が成り立つため、\(I_{uw\text{-}minusTu}\)は\(I_{uw\text{-}plusTu}\)、\(F_{pw}\)、\(F_{r1w}\)から導ける。
\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}+\displaystyle \frac{I_{uw\text{-}minusTu}}{NT_u}=\displaystyle \frac{F_{pw}}{N}+\displaystyle \frac{F_{r1w}}{N}\)
\(I_{uw\text{-}plusTu}+I_{uw\text{-}minusTu}=F_{pw}T_u+F_{r1w}T_u\)
ここで、
\(P_u=\displaystyle \frac{|I_{uw\text{-}plusTu}|}{|I_{uw\text{-}plusTu}|+|I_{uw\text{-}minusTu}|}\)
を考える。
\(P_u=0.5\)のときの理想の1完歩での後肢負重率を\(H_{u0}\)とする。
これが基本の後肢負重率になり、後肢負重率の変化量を\(\Delta H=H-H_{u0}\)とする。(理想の1完歩での早期負重度の変化量を\(\Delta H_u=H_u-H_{u0}\)とする。)
\(P_u\)が大きいほど\(H_u\)、\(\Delta H_u\)は大きくなる。
\(\displaystyle \frac{\partial}{\partial P_u} H_u \gt 0\) \((\displaystyle \frac{\partial}{\partial P_u}\Delta H_u \gt 0)\)
\(P_u \lt 0.5\)のとき、\(\Delta H_u \lt 0\)
\(P_u \gt 0.5\)のとき、\(\Delta H_u \gt 0\)

地面の変化による加速度補正数\(C\)の変化
加速度補正数\(C\)は地面(地面と足裏の接地部分の作用)によって変化する。
速く走れる地面ほど加速度補正数\(C\)は小さくなり、速く走れない地面ほど加速度補正数\(C\)は大きくなる。(原理や正確なことまではわかっていないので予想になる。)
競馬の芝レースでは、水分の少ない軽い馬場ほど\(C\)は小さくなり、水分を多く含んだ重い馬場ほど\(C\)は大きくなる。
(厳密には地面だけでなく蹄鉄にも左右される。)
ここから次のことが導かれ、それは私の目視での観察結果と矛盾しない。
・上り坂を一定の速度で走る場合など\(d_1 \gt d_2\)のときは、\(d_1\)と\(d_2\)が一定でも、速く走れない地面の場合の方が速く走れる地面の場合と比べて\(d\)が大きくなり、\(\Delta s_{ui}\,(i=1,…,n)\)が小さく、\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)が大きくなる。
・下り坂を一定の速度で走る場合など\(d_1 \lt d_2\)のときは、\(d_1\)と\(d_2\)が一定でも、速く走れない地面の場合の方が速く走れる地面の場合と比べて\(d\)は小さくなり、\(\Delta s_{ui}\,(i=1,…,n)\)が大きく、\(\displaystyle \frac{I_{uw\text{-}plusTu}}{NT_u}\)が小さくなる。

ドーピングの有無の見分け方についての予想
特殊な平均の力モデルと偽速度モデルを使ったドーピングの有無の見分け方はいくつか考えられるが、最も簡単なのがスパート中の各肢の早期負重度\(s_{ui}\)の変化の仕方から見分ける方法である。
この方法について、おおよそどのような原理になっているのか、単純なモデルを使って説明する。
わかっていないことが多く、厳密に正しくないかもしれない仮定を多用する点は注意が必要であるが、おおよそどのようなことが行われているかを示すことを目的としている。
まず単純化するために、地面は水平で変化せず、地面から受ける基本の力以外の受動的な力は働かず、真っすぐ走っている状況を想定する。
スパートを出力数が最大出力数\(B\)となること、スパート中を出力数が最大出力数\(B\)となっている時間の区間のこととする。実際には出力数が厳密に最大になることはないと思われるが、ここでは単純化して議論するためこのような定義とする。
スパート中は疲労するため走能力数\(A\)は減少する。
疲労以外では\(A\)は変化しないものとして、スパート中の\(A\)を、
\(A(t)=δt+A_0\) \((δ \leq 0)\)
\(δ\mathrm{\,[s^{-1}]}\) はスパート中であれば一定
と仮定する。
ただし、\(t\)はスパート中の時間であり、\(A_0\)は\(t=0\)のときの\(A\)である。
\(δ\)が小さい値であるほど疲労しやすいことを意味する。疲労しにくくなる効果のあるドーピングをしている個体とそうでない個体では、この\(δ\)に違いが現れ、ドーピングをしていると\(δ\)が極端に大きくなる(0に近くなる)。
地面が変化しないため、各肢の早期負重度\(s_{ui}\)の変化は、偽速度\(d\)の変化のみに依存する。よって、\(d\)の変化がわかれば、\(s_{ui}\)の変化もわかることになる。
スパート中の\(d\)の変化について考える。スパート中は常に\(d_2=0\)となる。また、
\(d_1(t)N=NA(t)h(B)+F_{r1x}(t)=ma_{ux}(t)\)
となるので、
\(d(t)N=Cd_1(t)N=Cma_{ux}(t)\)
\(d(t)=\displaystyle \frac{Cm}{N}a_{ux}(t)\)
\(a_{ux}(t)\)が求まれば、\(d(t)\)が求まる。
ここから\(a_{ux}(t)\)を求める。
まず、\(-F_{r1x}\)を\(v_{ux}\)と\(N\)に完全に比例するものと仮定して、
\(-F_{r1x}=εNv_{ux}\) \((ε \gt 0)\)
\(ε\mathrm{\,[s\,m^{-1}]}\) は定数
と置く。
こうすると、
\(a_{ux}(t)=\displaystyle \frac{NA(t)h(B)+F_{r1x}(t)}{m}\)
\(a_{ux}(t)=\displaystyle \frac{N(δt+A_0)h(B)-εNv_{ux}(t)}{m}\)
となり、下の微分方程式が得られる。
\(\displaystyle \frac{d}{dt}v_{ux}=-\displaystyle \frac{εN}{m}v_{ux}+\displaystyle \frac{δNh(B)}{m}t+\displaystyle \frac{NA_0h(B)}{m}\)
これを解くと、
\(v_{ux}=(v_{ux0}-\displaystyle \frac{A_0h(B)}{ε}+\displaystyle \frac{δmh(B)}{ε^2N})e^{-\frac{εN}{m}t}+\displaystyle \frac{δh(B)}{ε}t+\displaystyle \frac{A_0h(B)}{ε}-\displaystyle \frac{δmh(B)}{ε^2N}\)
\(v_{ux0}\)は\(t=0\)のときの\(v_{ux}\)である。
\(a_{ux}\)は、これを微分したものであるから、
\(a_{ux}=-\displaystyle \frac{εN}{m}(v_{ux0}-\displaystyle \frac{A_0h(B)}{ε}+\displaystyle \frac{δmh(B)}{ε^2N})e^{-\frac{εN}{m}t}+\displaystyle \frac{δh(B)}{ε}\)
\(a_{ux}=\displaystyle \frac{NA_0h(B)-εNv_{ux0}}{m}e^{-\frac{εN}{m}t}-\displaystyle \frac{δh(B)}{ε}(e^{-\frac{εN}{m}t}-1)\)
\(a_{ux}=\displaystyle \frac{NA_0h(B)+F_{r1x0}}{m}e^{-\frac{εN}{m}t}-\displaystyle \frac{δh(B)}{ε}(e^{-\frac{εN}{m}t}-1)\)
\(a_{ux}=a_{ux0}e^{-\frac{εN}{m}t}-\displaystyle \frac{δh(B)}{ε}(e^{-\frac{εN}{m}t}-1)\)
\(a_{ux0}\)は\(t=0\)のときの\(a_{ux}\)である。
\(d(t)\)は、
\(d(t)=\displaystyle \frac{Cm}{N}a_{ux}(t)=\displaystyle \frac{Cm}{N}(a_{ux0}e^{-\frac{εN}{m}t}-\displaystyle \frac{δh(B)}{ε}(e^{-\frac{εN}{m}t}-1))\)
となる。
ここで、地面は水平で地面から受ける基本の力以外の受動的な力は働かない状況のため、重力加速度を\(g\mathrm{\,[m\,s^{-2}]}\)すると、
\(N=mg\)
となる。そして、
\(d(t)=\displaystyle \frac{C}{g}a_{ux}(t)=\displaystyle \frac{C}{g}(a_{ux0}e^{-εgt}-\displaystyle \frac{δh(B)}{ε}(e^{-εgt}-1))\)
\(d\)、\(a_{ux}\)は、\(t\)、\(a_{ux0}\)、\(δ\)によって決まる。
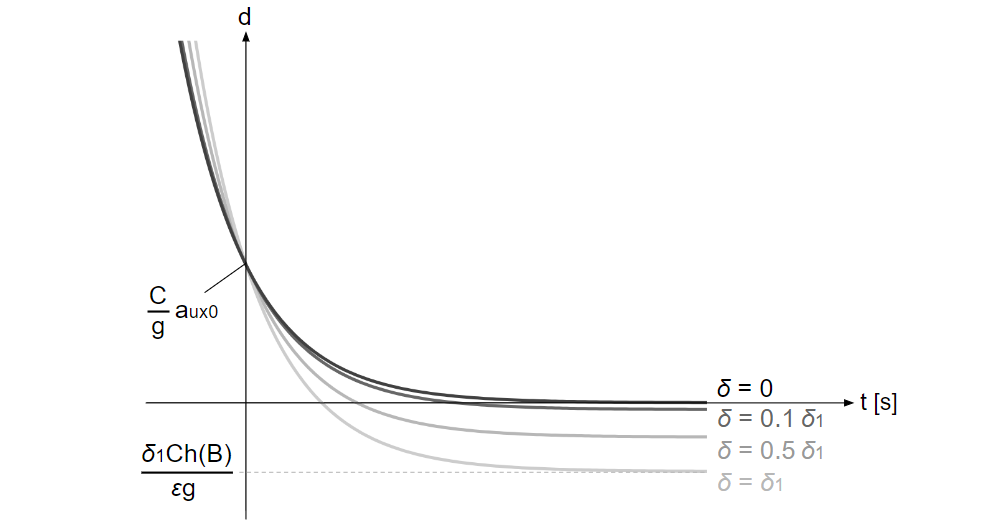
\(d\)の時間微分についても考える。
\(\displaystyle \frac{d}{dt}d(t)=\displaystyle \frac{C}{g} \displaystyle \frac{d}{dt}a_{ux}(t)=-C(εa_{ux0}-δh(B))e^{-εgt}\)
となる。
\(t=0\)のときは、
\(\displaystyle \frac{d}{dt}d=\displaystyle \frac{C}{g} \displaystyle \frac{d}{dt}a_{ux}=-C(εa_{ux0}-δh(B))\)
となる。
スパート中であれば、どこでも\(t=0\)にすることができる。つまり、\(d\)の時間微分\(\displaystyle \frac{d}{dt}d\)と地面から見た理想の1完歩での平均加速度の時間微分\(\displaystyle \frac{d}{dt}a_{ux}\)は、その時点の地面から見た理想の1完歩での平均加速度\(a_{ux}\)と\(δ\)によって決まり、
\(\displaystyle \frac{d}{dt}d=\displaystyle \frac{C}{g} \displaystyle \frac{d}{dt}a_{ux}=-C(εa_{ux}-δh(B))\)
と表せる。
スパート中の\(a_{ux}\)に対応する\(\displaystyle \frac{d}{dt}d\)と\(\displaystyle \frac{d}{dt}a_{ux}\)の大きさに着目すると、\(δ\)が大きい(0に近い)ほど\(\displaystyle \frac{d}{dt}d\)と\(\displaystyle \frac{d}{dt}a_{ux}\)が大きくなる(0に近くなる)ことがわかる。
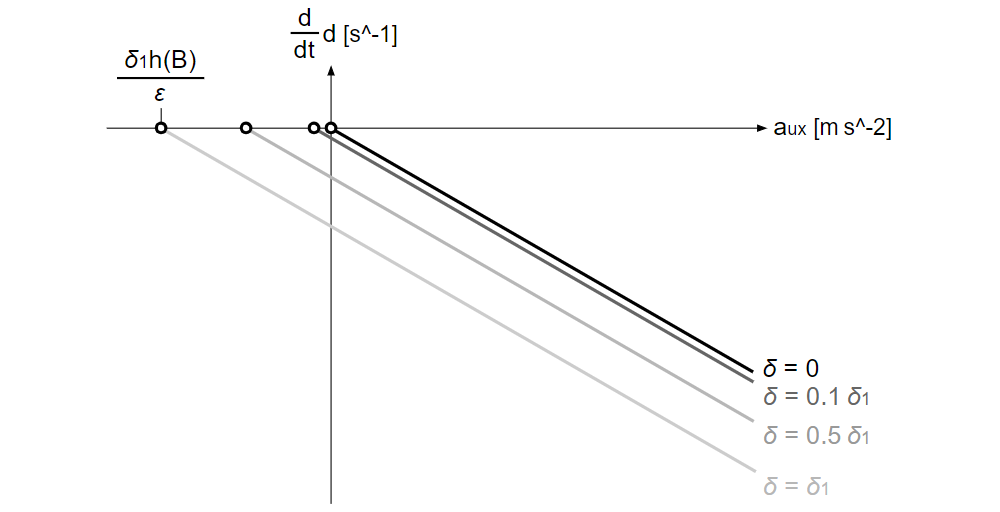
また、\(\displaystyle \frac{d}{dt}d\)が大きい(0に近い)ほど、\(\displaystyle \frac{d}{dt}s_{ui}\)は小さくなる(0に近くなる)。
疲労しにくくなる効果のあるドーピングをしていると\(δ\)が極端に大きくなる(0に近くなる)ため、\(a_{ux}\)に対応する\(\displaystyle \frac{d}{dt}a_{ux}\)、\(\displaystyle \frac{d}{dt}d\)が極端に大きくなり(0に近くなり)、\(a_{ux}\)に対応する\(\displaystyle \frac{d}{dt}s_{ui}\)が極端に小さくなる(0に近くなる)。
厳密に正しくないかもしれない仮定を用いたため、計算式がどこまで正確かはわからない。しかし、次のことは原理的にも正しいと思われる。
・疲労しにくくなる効果のあるドーピングの有無以外は同じ状態の人や馬が、同じ初期条件でスパートをしているとき、そのスパート中であればどの時間でも、地面から見た理想の1完歩での平均加速度\(a_{ux}\)、偽速度\(d\)、各肢の早期負重度\(s_{ui}\)の時間微分は、ドーピングを使用している方が0に近くなる。
厳密な言い方ではないが簡単に言うと、スパート中は疲労しにくくなる効果のあるドーピングをしていると、地面から見た理想の1完歩での平均加速度\(a_{ux}\)、偽速度\(d\)、各肢の早期負重度\(s_{ui}\)が変化しにくくなるということである。

ドーピングをしている走りの例
ちゃんと読んでいただけたでしょうか。まあ、数式を使ってウダウダと言いましたけど、実際に疲労しにくくなる系のドーピングをしている走りを見るのが手っ取り早いと思います。というわけで、ドーピングをしている走りの例を挙げておきます。
まずは、1988年オリンピック100mのベン・ジョンソン。そして、女子100m200mの世界記録を出したときのフローレンス・ジョイナー。女子400mの世界記録を出したときのマリタ・コッホ。目新しいところでは、2023年世界陸上100mと2024年オリンピック100mのシャカリ・リチャードソン。
ぜひドーピングしていない選手の走りと見比べてみてください。スパート中の早期負重度があまり変化しないことがわかると思います。
まあでもある程度走りを見ることに慣れていないと難しいかもしれません。どうでしょうか。私にはハッキリと違いがわかるんですが。
シャカリ・リチャードソンは現在まで、能力向上目的ではドーピング検査に引っかかったことはありません。ただ、走りを見る限りほぼ黒と言っていいでしょう。現状はさすがに走りだけで処分することはできませんが、走りからドーピングをしていると思われる選手は、検査の頻度を上げる&検体の長期保存をするというのが個人的には最適解かなと思います。
馬ではディープイン・・・これは次回以降にしておきます。

歩きについて
歩きでも走りと同様のことが起きると思っています。
人であれば歩きと走り、馬であれば常歩、速歩、駈歩、襲歩。この転移まで本当は組み込みたかったんですが、ドーピングの有無を見分けるという目的から離れてしまうので、一旦保留ということで。

疲れました
解説は以上です。やっぱりこういうことを考えるのは楽しいです。疲れたと言うと勘違いされそうですが、考えることに努力や苦痛などは何もありません。私にとって好きなことを好きなだけ考えられるというのは、中での生活において唯一とも言えるご褒美なのです。ただ、文章に起こしたり人に見せられるグラフを書いたりする作業は刑務作業よりも苦痛で、手を抜きながらですが私なりにかなりの努力をしたつもりです。がんばって、努力をしたので、自分にご褒美をあげたいですね。まあ、刑務所の中なんで考えることくらいしかできませんが。とほほ。




